Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 9.Problemas - Ex. 16

Sabendo que a viga A E   é um perfil de aço laminado 1200 x 27,4   e que P = 17,5   k N ,   L = 2,5   m ,   a = 0,8   m   e E = 200   G P a ,   determine (a) a equação da linha elástica para a parte B D   e (b) a deflexão o centro C   da viga.

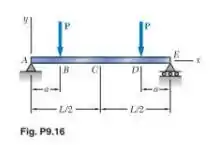
Passo 1

Fala aí, galera. Tudo bem? Partiu mais uma questão.

Neste tipo de questão, vamos utilizar a equação da linha neutra para acharmos a deflexão pedida.

Sabemos que a equação da linha neutra é dada por:

E I d 2 y d x 2 = M x

Logo, precisamos da equação do momento. Além disso, integrando a equação uma vez, temos a equação da rotação e, integrando duas vezes, temos a equação da deflexão. Todas as equações citadas acima são em função da distância x   axial à estrutura, indo da esquerda para a direita.

Para determinar a equação do momento, precisamos das reações. Neste caso, por simetria:

F A = F B = P

Passo 2

Agora, vamos separar a equação do momento em duas partes, para facilitar. Faremos da seguinte forma:

0 < x < a

E I d 2 y d x 2 = P x

Logo, integrando-se duas vezes para acharmos a equação da linha elástica.

E I d y d x = 1 2 P x 2 + C 1

E I   y = 1 6 P x 3 + C 1 x + C 2

Agora, faremos o mesmo para o outro trecho:

a < x < L - a

Neste trecho, teremos:

E I d 2 y d x 2 = P a

Logo, integrando duas vezes:

E I d y d x = P a x + C 3

E I   y = 1 2 P a x 2 + C 3 x + C 4

Passo 3

Para determinar as constantes de integração, vamos aplicar algumas condições de contorno. Como a deflexão nos apoios são sempre nulas:

x = 0 → y = 0

Logo:

C 2 = 0

Na metade da estrutura, a declividade (rotação) é nula, logo:

x = L 2 → d y d x = 0

Portanto:

C 3 = - 1 2 P a L

Também sabemos que a rotação em a   deve ser a mesma nas duas equações, logo:

x = a → d y d x = d y d x

Isto é:

1 2 P a 2 + C 1 = P a 2 - 1 2 P a L

C 1 = 1 2 P a 2 - 1 2 P a L

Por fim, sabemos que a deflexão em a   também deve ser a mesma nas duas equações, portanto:

x = a → y = y

Ou seja:

1 6 P a 3 + 1 2 P a 3 - 1 2 P a L = 1 2 P a 3 - 1 2 P a 2 L + C 4

C 4 = 1 6 P a 3

Passo 4

Pronto, já temos todas as incógnitas. Basta listar o que o problema pede. Na letra a ,   a equação da linha elástica para o trecho B D   será:

E I   y = 1 2 P a 2 + C 3 x + C 4

Substituindo:

y = P E I 1 2 a x 2 - 1 2 a L x + 1 6 a 3

Passo 5

Para a letra b, basta substituir a posição do ponto C   na equação da linha elástica. Logo:

x = L 2

y c = P E I 1 8 a L 2 - 1 4 a L 2 + 1 6 a 3

Substituindo os valores:

y c = 1,976   m m

Meu intuito aqui é auxiliar no raciocínio da questão, e não fazer contas. Logo, eu apenas substitui a força P ,   o módulo de alasticidade E   e as distâncias L   e a ,   todos fornecidos pelo enunciado. O momento de inércia I   pode ser encontrado procurando-se o perfil nos ábacos do fim do livro.

Até a próxima!

Resposta

  1. y = P E I 1 2 a x 2 - 1 2 a L x + 1 6 a 3
  2. y c = 1 , 976   m m
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para a viga e o carregamento mostrados nas figuras, determine (a) a inclinação na extremidade A, (b) a deflexão no ponto B e (c) a deflexão na extremidade D.
Para a viga e o carregamento mostrados nas figuras, determine (a) a equação da linha elástica, (b) a inclinação na extremidade A e (c) a deflexão do ponto C.
Para a viga e o carregamento mostrados nas figuras, determine as deflexões no (a) ponto B, (b) ponto C e no (c) ponto D.
Para a viga e o carregamento mostrados nas figuras, determine as deflexões no (a) ponto B, (b) ponto C e no (c) ponto D.
Para a viga e o carregamento mostrados nas figuras, determine (a) a equação da linha elástica, (b) a inclinação no ponto B e (c) a deflexão no ponto C.