Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 6.Problemas - Ex. 34
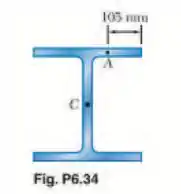
Sabendo que uma viga em perfil W360 x 122 de aço laminado está sujeita a uma força cortante vertical de 250 kN, determine a tensão de cisalhamento (a) no ponto A, (b) no centroide C da seção.
Passo 1
Tá legal! Nesse exercício temos um perfil de viga comercial, então vamos ter que ir lá no apêndice C pegar as informações pra ela, pois vamos precisar para os cálculos. Precisamos encontrar a tensão de cisalhamento no ponto A e no centroide C, e nós sabemos que a tensão de cisalhamento é dada por:
Em que V é a força cortante dada no enunciado, Q é o momento de área, I é o momento de inércia que vamos pegar do apêndice C e t é a espessura da seção em análise, outro dado que vamos tirar lá do apêndice C.
Passo 2
Tá legal! Vamos começar indo lá no apêndice C pegar as informações referente a nossa viga W360 x 122, onde teremos:
Em que I é o momento de inércia, d é a altura da viga, é a espessura da mesa, é a largura da mesa e é a espessura da alma. Beleza! Agora podemos começar de fato a letra (a). Vamos começar calculando o momento de área, dado por:
Agora vamos destacar a área A de interesse para que fique mais fácil calcular seu momento de área, fazendo isso, teremos:
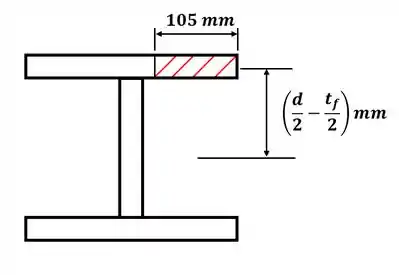
Observe que destacamos a distância entre o centroide da seção de interesse e o centroide da viga, pois vamos precisar dessa distância para calcular o momento de área. Então, podemos escrever como:
Substituindo os valores conhecidos, temos:
Agora, sabendo que a espessura da nossa área de interesse é a própria espessura da mesa, ou seja, , podemos calcular a tensão de cisalhamento através de:
Substituindo os valores conhecidos, teremos:
Shoow! A letra (a) já era. Vamos pra (b) agora.
Passo 3
Agora, para a letra (b), vamos desenhar a área de interesse, lembrando que agora temos que pegar tudo que está “acima” ou “abaixo” do ponto C, ou seja:
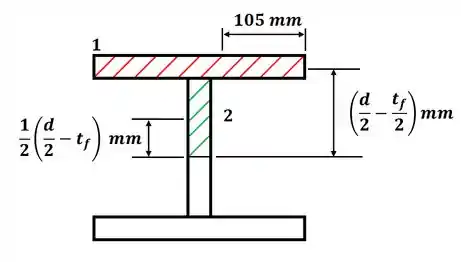
Note que já destacamos a distância entre o centroide da seção 1 e o centroide da viga e também a distância entre o centroide da seção 2 e o centroide da viga. Dessa forma, nosso momento de área será:
Substituindo os valores conhecidos, teremos:
Agora, sabendo que a espessura da nossa área de interesse no ponto C é a própria espessura da alma, ou seja, , podemos calcular a tensão de cisalhamento através de:
Substituindo os valores conhecidos, teremos:
E esse é o valor pedido na letra (b). Finalizamos por aqui!