Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 11.Problemas - Ex. 36

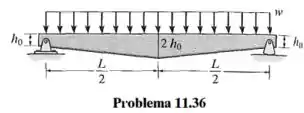
A viga mostrada na figura suporta uma carga distribuída uniforme w. Se for feita de uma chapa com largura constante b, determine a tensão de flexão máxima absoluta na viga.

Passo 1

Para resolver a questão precisamos aplicar a equação da flexão. Porém, o momento interno e a geometria da seção mudam com a distância. Então faremos o seguinte procedimento:

  • Calculamos as reações de apoio e encontramos uma equação para o momento fletor M ( x )
  • Encontramos uma equação para o momento de inércia I ( x )
  • Aplicamos a equação da flexão σ x = M x ⋅ c ( x ) I ( x )
  • Derivamos e igualamos a equação da flexão a zero para encontrar o ponto de máximo d σ x d x = 0
  • Utilizamos o valor encontrado para determinar a tensão máxima

Para facilitar nossas contas, vamos levar em consideração que a viga é simétrica, e consequentemente seus esforços e tensões são simétricos. Então faremos todos esses cálculos apenas para uma metade da viga!

Passo 2

Calculamos as reações de apoio:

∑ M B = 0 ⇒ - R A ⋅ L + w ⋅ L ⋅ L 2 = 0

R A = w L 2

∑ F Y = 0 ⇒ R A - w L + R B = 0

R B = w L 2

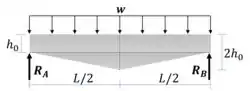
Passo 3

Vamos calcular uma equação pro momento fletor sobre a viga

∑ M = 0 ⇒ - R A x + w x 2 2 + M ( x ) = 0

M x = w L 2 2 x - w 2 x 2

M x = w 2 ( L x - x 2 )

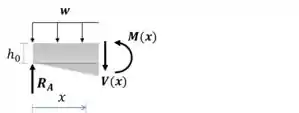
Passo 4

Vamos calcular as propriedades geométricas da seção:

c x = h x 2

I x = b ⋅ h x 3 12

Passo 5

Vamos definir uma função que represente a altura. Vamos nos concentrar e apenas metade seção:

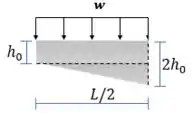
O comportamento da figura é linear. Então podemos aplicar uma regressão linear:

h x - h 0 x = 2 h 0 - h 0 L / 2

h x = 2 h 0 L x + h 0

Simplificando:

h x = h 0 L ( 2 x + L )

Passo 6

Vamos aplicar a equação da flexão:

σ x = M x ⋅ c x I x

σ x = w 2 ( L x - x 2 ) ⋅ h x 2 b ⋅ h x 3 12

σ x = 3 w ( L x - x 2 ) b ⋅ h x 2

Aplicando h ( x )

σ x = 3 w ( L x - x 2 ) b ⋅ h 0 L ( 2 x + L ) 2

σ x = 3 w L 2 b h 0 2 ⋅ ( L x - x 2 ) 2 x + L 2

Passo 7

Para encontrar o ponto máximo, vamos derivar a equação da flexão e igualar a zero

d σ x d x = 0

3 w L 2 b h 0 2 ⋅ L - 2 x 2 x + L 2 - L x - x 2 ⋅ 2 2 x + L ⋅ 2 2 x + L 4 = 0

Jogando o denominador e as constantes pro outro lado:

L - 2 x 2 x + L 2 - L x - x 2 ⋅ 2 2 x + L ⋅ 2 = 0

L - 2 x 2 x + L 2 - 4 L x - x 2 2 x + L = 0

Pondo em evidência:

2 x + L L - 2 x 2 x + L - 4 L x - x 2 = 0

Simplificando:

2 x + L ( L 2 - 4 L x ) = 0

Resolvendo, termos dois resultados:

x = - L 2

x = L 4

Vamos desconsiderar o valor negativo:

x m a x = L 4

Passo 8

Finalizamos a questão aplicando o valor x m a x na equação da flexão:

σ x m a x = 3 w L 2 b h 0 2 ⋅ ( L x m a x - x 2 ) 2 x m a x + L 2

σ m a x = 3 w L 2 b h 0 2 ⋅ L L 4 - L 4 2 2 L 4 + L 2

σ m a x = w L 2 4 b h 0 2

Resposta

x m a x = L 4

σ m a x = w L 2 4 b h 0 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

148. Duas forças são aplicadas a um tubo A B , como mostrado. Sabendo-se que o tubo tem diâmetros, interno e externo, iguais a 35m m e 42m m , respectivamente, determinar as tensões, normal e de cisal
149. Resolver o problema 5.148 , considerando que a força de 1500N é dirigida para cima
As fibras de uma peça de madeira formam um ângulo de 18 graus com a vertical. Para o estado de tensões mostrado determinar: (a) a tensão de cisalhamento no plano, em um plano paralelo as fibras;(b) a
Duas peças de madeira de 80x120mm, de seção transversal retangular e uniforme, são unidas por simples colagem das seções chanfradas, como mostrado. Sabendo-se que as máximas tensões admissíveis na jun
Um tubo de aço de 300mm de diâmetro externo é fabricado com chapa fina de 6,35mm de espessura, soldada ao longo de uma hélice que forma um ângulo de 22,5 graus com um plano perpendicular ao eixo do tu