Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 7.Problemas - Ex. 54

Determinar as equações das curvas dos diagramas de força cortante e de momento fletor, para a viga com o carregamento mostrado. Determinar o máximo valor absoluto do momento fletor na viga.

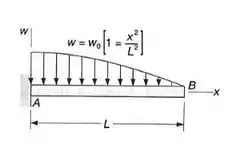
Passo 1

E ai gurizada tudo beleza? Espero que sim!!

Para calcularmos o momento fletor, temos que fazer as seguintes etapas vem comigo ;)

d V d X = W = W o 1 - x 2 / L ²

V = W o 1 - x 3 3 L ² + C

Se V=0 e x=L substituindo temos...

0 = + C

C = W o - W o L 3 3 L ²

V = W o - W o x 3 3 L ² + W o - W o L 3 3 L ²

Agora a gente dá aquela ajeitadinha na equação para deixa-la bonitinha

V = ( W o × L 3 ) × ( 2 - 3 x L + x L 3 )

Passo 2

Agora devemos encontrar o momento, entãoo faremos isso ;)

d M d X = V = ( W o × L 3 ) × ( 2 - 3 x L + x L 3 )

M = W o × L 3 × ( 2 x - 3 x ² 2 L + x 4 L 4 )

M = W o × L 12 × ( 2 x - 3 x ² 2 L + x L 4 )

Agora a gente dá aquela ajeitadinha na equação para deixa-la bonitinha

M = W o × L ² 12 × ( 3 - 8 x L + 6 x L 2 - x L 4 )

Passo 3

Para acharmos o momento máximo vamos considerar que:

Vamos substituir : M=0 em x=L

0 = W o × L ² 12 × ( 3 - 8 L L + 6 L L 2 - L L 4 )

M m á x = W o × L ² 12 × ( 3 - 8 L L + 6 L L 2 - L L 4

M m á x = W o × L ² 12 × ( 3 - 8 L + 6 L 2 - L 4 L

M m á x = W o 4 × 8 L ³ + 6 L 4 - L 6 L

M m á x = W o 4 × L ²

Resposta

M m á x = W o 4 × L ²

.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para a viga com o carregamento mostrado, determinar: a) máximo valor absoluto do momento fletor b) máxima tensão normal devido à flexão.
Para a viga com o carregamento mostrado, determinar: a) o máximo valor absoluto d momento fletor b) maior tensão normal devido à flexão.
Para a viga com o carregamento mostrado, determinar: a) máximo valor absoluto do momento fletor b) máxima tensão normal devido à flexão.
Para a viga com o carregamento mostrado, determinar: a) máximo valor absoluto do momento fletor b) máxima tensão normal devido à flexão.
Para a viga com o carregamento mostrado, determinar: a) máximo tensão normal devido a flexão b) maior tensão de cisalhamento numa seção transversal devido à flexão.