Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 6.Problemas - Ex. 118
Para a seção, Iy’ = 31,7(10-6)m4, 12, Iz’ = 114(10-6)m4, Iy'z' = 15,1(10-6)m4. Usando as técnicas apresentadas no Apêndice A, a área da seção transversal do elemento tem momentos principais de inércia IY = 29,0(10-6)m4 e Iz= 117(10-6)m4, calculados em torno dos eixos principais de inércia y e z, respectivamente. Se a seção for submetida a um momento M = 2.500 N · m direcionado como mostra a figura, determine a tensão produzida no ponto A, através da equação σ = [-(MzIy+MyIyz)y +(MyIz+MzIyz)z]/(IyIz-Iyz²).
Passo 1
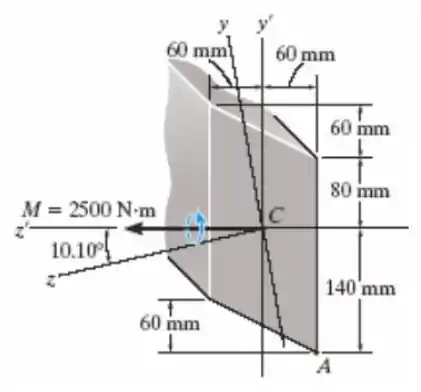
Faaaala, meu povo bonito!! Tudo bem com vocês?? Nossa questão de hoje já chegou fazendo carinho e nos dando os principais elementos da noite: os momentos de inércia, tanto para o eixo cartesiano clássico, quanto para o eixo rotacionado de 10,10º. O que ele nos pede é para calcular a tensão produzida no ponto A quando essa seção receber um momento aplicado na horizontal igual a 2500 N.m. Sacou??
Passo 2
Bom, ele já nos dá até a fórmula para usarmos e também nos disse o valor de Mz. Como ele está inteiro no eixo z, não teremos sua componente vertical, ou seja, My = 0. Agora, é só substituir e partir pro abraço!!