Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 6.Problemas - Ex. 83
Determine as componentes horizontal e vertical da reação que os pinos A e C exercem sobre o arco de dois membros.
Passo 1
Desenhando o diagrama do corpo livre dos dois trechos AB E BC da peça:
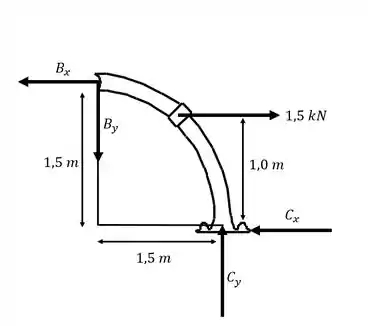
Passo 2
Podemos começar escrevendo a equação do equilíbrio em relação ao momento em relação ao ponto A no membro AB e em relação ao ponto C no membro BC:
Resolvendo o sistema:
Passo 3
Para o membro AB, aplicamos as equações do equilíbrio de forças nos eixos x e y:
Passo 4
Para o membro BC, aplicamos as equações do equilíbrio de forças nos eixos x e y:
Resposta
Exercícios de Livros Relacionados
6.114. A pá do trator transporta uma carga de 500k g de terra, com centro de massa em G. Calcule as forças desenvolvidas nos cilindros hidráulicos IJ e BC devido a essa carga.
6.116. Se a força de prensagem horizontal que o grampo exerce sobre o bloco liso de madeira em E é N E = 200N , determine a força P aplicada no cabo do grampo articulado.
6.113. Mostre que o peso W 1 do contrapeso em H necessário para o equilíbrio é W 1 = b a ⋅ W e portanto, ele é independente da posição da carga W na plataforma.
6.115. Se uma força P = 100N é aplicada no cabo do grampo articulado, determine a força de prensagem horizontal N E que o grampo exerce sobre o bloco liso de madeira em E.
6.109. Se uma força de prensagem de 300N é necessária em A, determine a quantidade de força F que precisa ser aplicada no cabo do grampo articulado.