Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 6.Problemas - Ex. 84
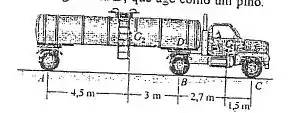
O caminhão e o tanque possuem pesos de 40 kN e 100 kN respectivamente. Seus centros de gravidade respectivos são localizados nos pontos G1 e G2 . Se o caminhão está em repouso, determine as reações em ambas as rodas em A, em B e em C. O tanque está conectado ao caminhão na plataforma giratória D, que age como um pino.
Passo 1
Falaaa! Então vamos entender o que está acontecendo aí. Ele quer as reações nas rodas. Mas ele diz que em há um pino, então a gente pode separar essa estrutura toda em duas: o tanque e o caminhão.
Só temos que ter atenção a duas coisas:
- a gente precisa começar pela parte que não consegue ficar em pé sozinha, porque isso nos ajuda a resolver as equações de forma mais simples.
Na nossa situação, podemos interpretar que o tanque está apoiado numa roda e a outra extremidade está presa ao caminhão pelo pino. Se a gente tira o caminhão, o tanque tomba, então vamos começar por ele. Aí a gente descobre todas icógnitas em um e depois no outro.
- uma das forças de reação do tanque é a dada pela roda, e a outra é dada pela estrutura do caminhão, através do pino. Por isso no DCl do caminhão a gente precisa colocar forças representando que ele também serve de reação para o tanque.
No DCL do caminhão, as reações do tanque aparecem com a mesma direção e sentidos opostos.
Tendo pensado nessas coisinhas, a gente pode começar!
Passo 2
Podemos começar desenhando o diagrama do corpo livre do tanque:
Como ali em nós temos um pino, ele vai gerar reações nas duas direções.
Passo 3
Aplicando as equações de equilíbrio de forças nos eixo x e y:
Passo 4
Aplicando as equações do equilíbrio em relação ao momento para o ponto D para o tanque:
Achamos tudo do tanque. Vamos para o caminhão!
Passo 5
Desenhando o DLC do caminhão:
Repara que a gente colocou e nele com sentidos opostos ao que aparece no DCL do tanque.
Passo 6
Aplicando aas equações do equilíbrio em relação ao momento para o ponto D:
Passo 7
Aplicando as equação de equilíbrio de forças no eixo y: