Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 8.Problemas - Ex. 137

Para ser de uso prático, o dispositivo de segurança descrito no problema anterior deve deslizar livremente ao longo do trilho quando puxado para cima. Determine o maior valor admissível do coeficiente de atrito estático entre a flange do trilho e os pinos A e B , para que a manga fique livre para deslizar quando puxada como mostra a figura, considerando a   θ = 60 ° , b   θ = 50 ° , c   θ = 40 ° .

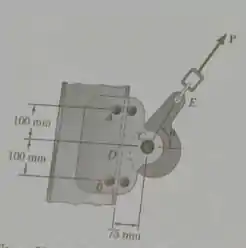
Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

Vamos analisar o seguinte diagrama:

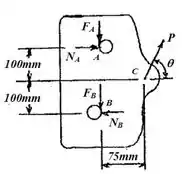
Vamos calcular o momento em C :

∑ M C = 0

F A 0,075 + F B 0,075 + N A 0,1 - N B 0,1 = 0

μ s N A 0,075 + μ s N B 0,075 + N A 0,1 - N B 0,1 = 0

μ S = 0,1 0,075

μ s = 1,3333

Passo 2

Vamos verificar, agora, se a suposição é correta com relação ao momento dado no mecanismo através do somatório de forças na horizontal e vertical:

∑ F x = 0

N A - N B + P cos ⁡ θ = 0

N B - N A = P cos ⁡ θ

Agora analisando verticalmente, temos:

∑ F y = 0

- μ s N A - μ s N B + P sen ⁡ θ = 0

μ s N A + μ s N B = P sen ⁡ θ

Logo:

N A + N B = P sen ⁡ θ μ s  

Passo 3

Como N A = N B - P cos ⁡ θ , temos que:

N B - P cos ⁡ θ + N B = P sen ⁡ θ μ s

2 N B = P cos ⁡ θ + P sen ⁡ θ μ s

N B = P 2 cos ⁡ θ + sin ⁡ θ μ s

Da mesma forma podemos encontrar N A :

N A = P 2 cos ⁡ θ + sin ⁡ θ μ s - P cos ⁡ θ

N A = P 2 sin ⁡ θ μ s - cos ⁡ θ

Passo 4

Como os resultados acima devem ser positivos, teremos a condição de achar o ângulo correspondente à força P no qual possui valor admissível do coeficiente de atrito estático entre o falnge do trilho e os pinos:

tan ⁡ θ ≥ μ s

θ = tan - 1 ⁡ 1,3333

θ = 53,13 °

Portanto podemos afirmar que para θ = 60 ° existe o contato e μ s = 1,333 .

Agora vamos determinar o coeficiente onde o contato não ocorre:

∑ F x = 0

- N A - N B + P cos ⁡ θ = 0

N B + N A = P cos ⁡ θ

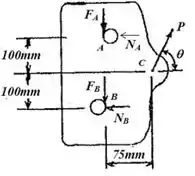
Agora analisando verticalmente, temos:

∑ F y = 0

- μ s N A - μ s N B + P sen ⁡ θ = 0

μ s N A + μ s N B = P sen ⁡ θ

Logo:

N A + N B = P sen ⁡ θ μ s  

Igualando teremos:

P sen ⁡ θ μ s = P cos ⁡ θ

Logo:

μ s = tan ⁡ θ

Passo 5

Agora é só substituir os ângulos:

Para θ = 50 ° :

μ s = tan ⁡ 50 °

μ s = 1,192

Para θ = 4 0 ° :

μ s = tan ⁡ 4 0 °

μ s = 0,839

Resposta

a )   μ s = 1 , 333

b )   μ s = 1,192

c )   μ s = 0,839

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Se uma força P = 30N for aplicada ao cabo da alavanca, determine o maior momento de binário M que pode ser resistido de modo que a roda não gire. O coeficiente de atrito estático entre a correia e a r
Mostre que a relação de atrito entre as trações na correia, o coeficiente de atrito m e os contatos angulares α e β para a correia em “ V ” é T 2 = T 1 e μ β / sen ⁡ ( α / 2 ) .
Um cabo é preso à placa B de 20k g , passa por um pino fixo em C e é preso ao bloco em A .Usando os coeficientes de atrito estático mostrados, determine a menor massa do bloco A que impeça o movimento
Determine a força P que deverá ser aplicada ao cabo da alavanca para que a roda esteja na iminência de girar se M = 300N ⋅ m . O coeficiente de atrito estático entre a correia e a roda é μ s = 0,3 .
A corda suportando o cilindro de 6k g passa por três pinos, A ,B ,C , onde μ s = 0,2 . Determine a faixa de valores para a intensidade da força horizontal P para a qual o cilindro não subirá nem desce