Enunciado

Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 8.Problemas - Ex. 94

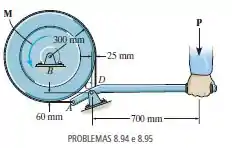
Determine a força que deverá ser aplicada ao cabo da alavanca para que a roda esteja na iminência de girar se . O coeficiente de atrito estático entre a correia e a roda é .

Passo 1

Show de bola galerinha, sabemos que as tensões da correia nos pontos de contato se relacionam através da fórmula:

Onde é o ângulo de abraçamento do cabo, dado por enquanto que é o coeficiente de atrito entre o cabo e a roda, dado como , sendo assim, segue que:

Passo 2

Iradoso, então já descobrimos a relação entre as tensões que passam pelo cabo, agora podemos calcular o momento em relação ao centro da roda dado como:

Então se a gente substituir a nossa relação, teremos:

Logo será:

Passo 3

Belezera, agora que sabemos todas as forças atuando no sistema, podemos calcular o momento em relação ao ponto , tal que:

Logo, isolando :

Portanto, será dado como:

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um eixo excêntrico de 100 mm de raio mostrado na figura é usado para controlar o movimento da placa CD. Sabendo que o coeficiente de atrito estático entre o excêntrico e a placa é 0,45, e desprezando

No Problema 8.30, determine o intervalo de intensidade dos valores da força vertical P aplicada em E para a qual a placa se moverá para baixo.

A placa ABCD de 225 N é ligada em A e D aos colares que podem deslizar sobre a barra vertical. Sabendo que o coeficiente de atrito estático entre os colares e a barra é 0,40, determine se a placa está

Resolva o Problema 8.32 considerando que o diâmetro do tubo é 30 mm.

Um tubo de 60 mm de diâmetro é apertado pela chave inglesa mostrada na figura. As partes AB e DE da chave são rigidamente ligadas entre si e a parte CF é conectada por um pino em D. Se a chave deve ap