Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 8.Problemas - Ex. 135

Uma barra delgada de comprimento L está apoiada entre um pino C e a parede vertical e sustenta uma carga P na extremidade A . Sabendo que o coeficiente de atrito estático entre o pino e a varra é 0,15 e desprezando o atrito no rolo, determine o intervalo de valores da razão L / a para a qual o equilíbrio é mantido.

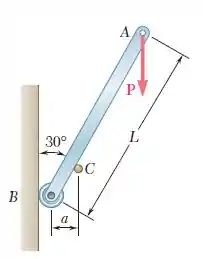
Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

Vamos analisar o diagrama de corpo livre da haste para o movimento de B sendo iminenete para cima:

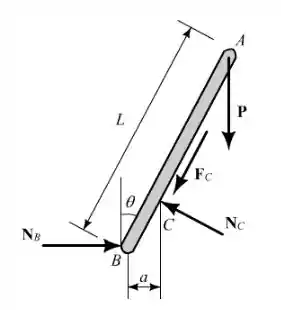
Vamos calcular o momento em B :

∑ M B = 0

N C a sen ⁡ 30 ° - P L sen ⁡ 30 ° = 0

N C = P L a sen 2 ⁡ 30 °

Passo 2

Suponha que a força na direção positiva do eixo y seja positiva.

∑ F y = 0

N C sen ⁡ 30 ° - F C cos ⁡ 30 ° - P = 0

Onde:

F C = μ s N C

F C = 0,15 N C

Logo:

P = N C sen ⁡ 30 ° - 0,15 cos ⁡ 30 °

P = 0,37 N C

Resolvendo para N C , temos:

N C = P 0,37

Passo 3

Agora que temos:

N C = P L a sen 2 ⁡ 30 °

E:

N C = P 0,37

Vamos igualar as duas funções:

P L a sen 2 ⁡ 30 ° = P 0,37

Teremos que:

L a = 1 0,37 sen 2 ⁡ 30 °

L a = 10,81

Passo 4

Agora vamos considerar o movimento de B sendo iminente para baixo. A sensação de força de atrito F C será revertida. Teremos μ S = - 0,15 .

Vamos fazer os mesmos cálculos do Passo 2 :

∑ F y = 0

N C sen ⁡ 30 ° - F C cos ⁡ 30 ° - P = 0

Onde:

F C = μ s N C

F C = - 0,15 N C

Logo:

P = N C sen ⁡ 30 ° + 0,15 cos ⁡ 30 °

P = 0 , 63 N C

Resolvendo para N C , temos:

N C = P 0 , 63

Passo 5

Teremos então que:

P L a sen 2 ⁡ 30 ° = P 0 , 63

Teremos que:

L a = 1 0 , 63 sen 2 ⁡ 30 °

L a = 6,35

Portatnto, a faixa de valores da razão L / a para a qual o equilíbrio é mantido é:

6,35 ≤ L a ≤ 10,81

Resposta

6,35 ≤ L a ≤ 10,81

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Os blocos A e B têm massas de 20 kg e 10 kg, respectivamente. Usando os coeficientes de atrito estático indicados, determine a maior massa do bloco D sem causar movimento.
A roda está sujeita a um torque de M=50Nm . Se o coeficiente de atrito cinético entre a cinta de freio e a borda da roda é u k=0,3 , determine a menor força horizontal P que deverá ser aplicada à alav
Uma correia transportadora é usada para transferir material granular e a resistência ao atrito no topo da correia é F=500N . Determine o menor alongamento da mola presa ao eixo móvel da polia livre B
Um motor de 20k g tem um centro de gravidade em G e está conectado por um pino em C para manter uma tração pré-tensionadora na correia propulsora. Determine o menor torque M em sentido anti-horário qu
A correia na secadora de roupas contorna o tambor D, a polia livre A e a polia do motor B. Se o motor pode desenvolver um torque máximoM=0,80N m , determine a menor tração da mola necessária para evit