Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 4.Problemas - Ex. 16
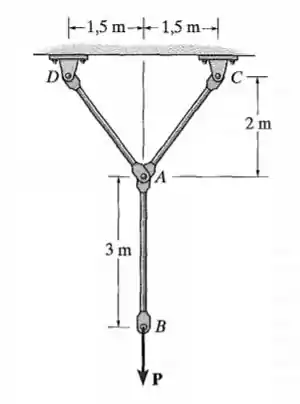
O sistema articulado é composto por três elementos de aço conectados por pinos, cada um com área de seção transversal de . Se uma força vertical for aplicada à extremidade do elemento , determine o deslocamento vertical do ponto .
Passo 1
Fala, querido! Desejamos encontrar o alongamento vertical do ponto dado o valor da força descrita no problema.
Precisamos começar, vamos lembrar que o alongamento em uma barra dado por uma força aplicada é:
Essa força aplicada em vai causar alongamento nas barras DA, CA e AB. Para achar o alongamento em cada barra, precisamos do comprimento de cada barra. E a força precisa estar na direção a barra. Normal a seção transversal da barra.
Aí reparamos que as barras apresentam um inclinação, então, vemos que vai ser preciso decompor a força força em duas componentes, na qual apenas a componente vertical nos interessa. E que precisamos calcular o comprimento dessas barras assim:
Além disso o ângulo de inclinação vai ser dado por
Esse é ângulo entre e vertical.
Com essas coisinhas pensadas, vamos achar as forças para cada barra. Vem!
Passo 2
Pelo desenho, a força em AB é mesmo, porque ela já está na direção da nossa barra. Assim,
O alongamento fica:
Aí falta achas as forças nas outras barras. Das equações de equilíbrio tiramos que
Da geometria do problema percebemos que , dessa forma
Agora vamos para o alongamento. Por causa da simetria da figura e do carregamento. E como todas as barra são do mesmo material, temos que
Passo 3
Vamos entender como o ponto se desloca verticalmente.
Dado que o ponto se desloca devido ao alongamento, podemos estabelecer um novo ponto e, então, fechamos um triângulo e teremos
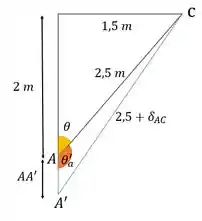
Com , isso vai ser importante para conseguirmos encontrar a deformação em , porque precisamos achar .
Podemos usar lei dos cossenos:
Aí a gente resolve essa equação do segundo grau e acha:
E o deslocamento vertical de vai ser esse deslocamento vertical de mais o alongamento de :