Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 4.Problemas - Ex. 65
A roda está sujeita à força de transmitida pelo eixo. Determine a força em cada um dos três raios. Considere que o aro é rígido, que os raios são feitos do mesmo material e que cada um tem a mesma área de seção transversal.
Passo 1
Um aro rígido está conectado por três raios (hastes) a um eixo no centro (em ). Uma força de para baixo é aplicada em .
Características dos raios , e:
- Comprimento inicial: .
- Módulo de elasticidade: . (conhecido!)
- Área: . (conhecido!)
O forçamento de irá puxar o ponto para baixo, alongando o raio e comprimindo os raios e .
Queremos a força em cada raio.
Passo 2
Diagrama de corpo livre.
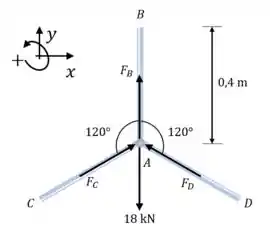
A simetria do problema irá facilitar nosso trabalho. Veja o equilíbrio de forças na horizontal:
Agora vejamos o equilíbrio na vertical:
Duas incógnitas ( e ), uma equação. Temos que formular a condição de compatibilidade para achar outra equação.
Passo 3
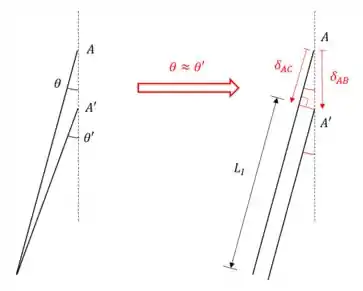
Por causa do forçamento, o raio vai ser esticado (deformação) um comprimento . O ponto vai descer, então em tese o ângulo vai mudar para algum . Mas como estamos sempre assumindo pequenas deformações, essa mudança no ângulo é desprezível: .
Com a aproximação, as retas são praticamente paralelas, e aí a diminuição do raio () fica visível em relação ao deslocamento .
Pelo triângulo formado, e como (figura no Passo 2), temos que
Show, essa era a parte difícil! Só falta aplicar fórmula.
Passo 4
Use a fórmula da relação carga-deslocamento
Aplicando essa relação na equação que obtemos pelo equilíbrio:
Resposta
Força no raio : .
Força no raio : .
Força no raio : .