Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 4.Problemas - Ex. 58
O conjunto é composto por dois postes do material com módulo de elasticidade e cada um com área de seção transversal e um poste do material com módulo de elasticidade e área de seção transversal . Se uma carga central for aplicada à tampa rígida, determine a força em cada material.
Passo 1
Temos uma estrutura feita de 3 postes: um em cada canto com material , e um no centro com material . Não tem valores nessa questão, então vamos definir as variáveis.
Características dos postes e :
- Área transversal: .
- Módulo de elasticidade: .
- Comprimento inicial: .
- Área transversal: .
- Módulo de elasticidade: .
- Comprimento inicial: .
Características dos postes :
Um forçamento vertical é imposto no meio da estrutura.
Até aqui, todas essas variáveis são conhecidas.
Queremos a força em cada poste. Vamos ver que nos postes de mesmo material, a força é a mesma, por causa da simetria.
Passo 2
Diagrama de corpo livre:
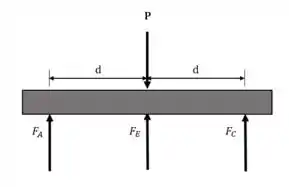
Fazendo o equilíbrio de momentos para o centro da estrutura:
Beleza. Vamos simplificar então e usar e .
Equilíbrio de forças:
Precisamos de mais uma equação!
Passo 3
A tampa é rígida, e por causa da simetria (, a força vai fazer ela descer sem se inclinar. Então o deslocamento de qualquer um dos postes de material tem que ser igual ao deslocamento do poste de material :
Use a fórmula da relação carga-deslocamento:
Passo 4
Vamos definir as forças e baseado nas variáveis que conhecemos
Voltando , encontramos a força que falta
Resposta
Força no material :
Força no material :