Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 4.Problemas - Ex. 59
O conjunto é composto por dois postes e do material com módulo de elasticidade e área de seção transversal cada e um poste central do material com módulo de elasticidade e área de seção transversal . Se os postes e tiverem de ser substituídos por postes do material , determine a área da seção transversal exigida para esses novos postes de modo que ambos os conjuntos sofram o mesmo grau de deformação quando carregados.
Passo 1
Temos uma estrutura feita de 3 postes. O conjunto consiste em: um poste em cada canto com material , e um poste no centro com material . O enunciado pede que investiguemos também um conjunto para a estrutura: todos os três postes com material .
Não tem valores nessa questão, então vamos definir as variáveis.
Conjunto :
- Características dos postes e :
- Área transversal: .
- Módulo de elasticidade: .
- Comprimento inicial: .
- Características dos postes :
- Área transversal: .
- Módulo de elasticidade:
- Comprimento inicial: .
- Características dos postes e :
- Área transversal: (nova área!)
- Módulo de elasticidade: .
- Comprimento inicial: .
- Características dos postes :
- Área transversal: .
- Módulo de elasticidade:
- Comprimento inicial: .
Conjunto :
Nos dois casos, um forçamento vertical é imposto no meio da estrutura. O forçamento causa uma deformação nos postes, comprimindo-os.
Todas essas variáveis são conhecidas com exceção de !
Muita informação! Vamos com calma.
A questão quer que achemos o valor da área para os postes e no caso do conjunto . Essa área deve garantir que o conjunto (sofra a mesma deformação que o conjunto (). Como todos os postes tem o mesmo comprimento inicial , podemos tratar só dos deslocamentos:
Primeiro, precisamos saber o quanto desloca em cada caso. Fórmula da relação carga-deslocamento:
Show, só não sabemos as forças nessa fórmula. Vamos achar isso para cada caso.
Passo 2
Diagrama de corpo livre:
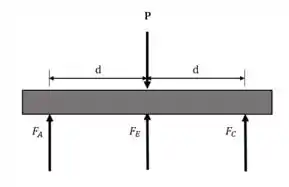
Fazendo o equilíbrio de momentos para o centro da estrutura:
Equilíbrio de forças:
Essas equações servem tanto pro conjunto quanto pro conjunto . Pra achar o valor das forças, porém, vamos precisar de mais uma equação.
Passo 3
A tampa é rígida, e por causa da simetria (, a força vai fazer ela descer sem se inclinar. Então o deslocamento dos postes tem que ser sempre igual.
Essa condição de compatibilidade vai servir para os dois conjuntos.
Passo 4
Vamos resolver primeiro para o caso do conjunto .
Agora podemos ver o deslocamento do conjunto :
Passo 5
Façamos o mesmo para o conjunto (confira de novo o Passo 1 para não se confundir!)
Calcule o deslocamento do conjunto :
Passo 6
Finalmente, vamos fazer o que o enunciado quer e forçar
Tudo ali é conhecido, menos o . Vamos isolar esse cara e aí teremos achado o valor dele que garante que . Corta , corta e inverte:
Resposta
Área exigida: