Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 4.Problemas - Ex. 143

Substitua o carregamento distribuído por uma força resultante equivalente e especifique sua posição na viga, medindo a partir de .

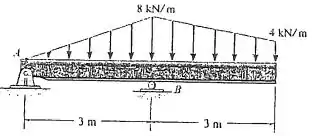
Passo 1

Existem duas formas de calcular a força resultante equivalente. A primeira é por integral, mas isso não é necessário já que são carregamentos triangulares e trapezoidais.

Então vamos prosseguir da seguinte maneira. Primeiro vamos dividir o carregamento trapezoidal em dois carregamentos, um uniforme (que tem o desenho de um retângulo) e outro triangular que ficará. Ambos vão atuar na mesma seção da barra. Então a gente vai ter isso aqui olha só:

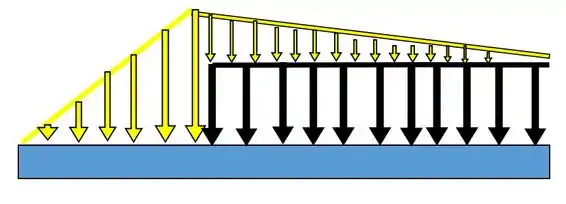
Então nós vamos ter os dois carregamentos triangulares (amarelos) mais o carregamento uniforme (preto).

Passo 2

Então a gente vai precisar calcular a força equivalente de cada um e somar todas. Vamos começar pelo carregamento uniforme que é mais simples. A força equivalente será igual ao carregamento vezes a distância:

A distância é e o valor do carregamento é igual a , por que 4? Porque o valor mais baixo do carregamento trapezoidal =D

Teremos, portanto:

Além disso o ponto onde essa força atua é exatamente no meio do carregamento, logo irá aturar em:

obs: Tivemos de somar 3 porque queremos a posição na viga como um todo.

Passo 3

Agora vamos calcular o carregamento triangular da esquerda. Para carregamentos triangulares a gente pode fazer uma média entre o menor e maior valor e multiplicar essa média pelo comprimento do carregamento (isso vale porque é uma variação linear)

Para o nosso caso:

Para todo carregamento a força irá atuar no baricentro da figura. Como temos um carregamento triangular o baricentro do triângulo é localizado a 2/3 da ponta do trinângulo (ou 2/3 da base) conforme o desenho:

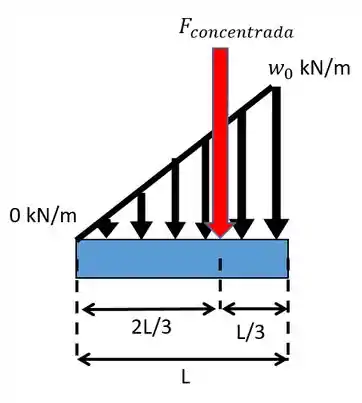
Dessa forma o ponto onde a força será aplicada será:

Passo 4

Agora vamos fazer a mesma coisa do passo anterior mas para o carregamento triangular da direita:

Mas aqui é muito importante notar que, como dividimos o carregamento trapezoidal, agora e ao invés de 8 e 4, beleza? Então vamos ter

E aqui a força irá atuar em:

Passo 5

Agora vamos juntar tudo que vimos

Para o carregamento uniforme:

Para o triangular da esquerda:

Para o triangular da direita:

Então a força resultante terá o valor de:

Passo 6

E para achar sua posição vamos calcular o momento que cada força faz com relação a um ponto qualquer (vamos escolher o ponto A) e depois ver qual distância a força resultante deverá atuar para possuir o mesmo momento, da seguinte forma: