Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 5.Problemas - Ex. 86

A barragem de um lago é projetada para suportar a força adicional causada pelo lodo depositado no fundo do lago. Admitindo que o lodo é equivalente a um liquido de densidade ρ s = 1,76 ⋅ 10 3   k g / m 3 e considerando uma seção da barragem de 1   m de largura, determine o aumento percentual da força exercida sobre a face da barragem para um acúmulo de lodo de 2   m de profundidade.

Passo 1

Bom galera, a gente vai começar fazendo um diagraminha de corpo livre da barragem sem o lodo, pra nortear a gente:

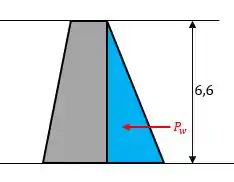
Passo 2

Vamos lá, a gente pode calcular a força de pressão exercida pela água horizontalmente na barragem, bem assim:

P W = 1 2 A ρ W = 1 2 A ρ g h

→ P W = 1 2 6,6 1 10 3 9,81 6,6

→ P W = 213,66   k N

Passo 3

Bom, agora, vamos analisar a situação com o lodo, vamos logo fazer um diagrama de corpo livre rapidinho:

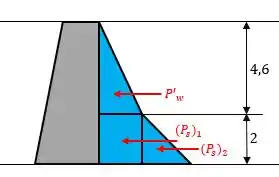
Passo 4

Agora, vamos calcular as forças de pressão exercidas pelos fluidos:

P = 1 2 A ρ g h

Calculando:

P W ' = 1 2 4,6 1 10 3 9,81 4,6 = 103,79   k N

P S 1 = 1 2 2 1 10 3 9,81 4,6 = 90,252   k N

P S 2 = 1 2 2 1 1,76 ⋅ 10 3 9,81 2 = 34,531   k N

Então, a soma dessa pressões fica:

P ' = 103,79 + 90,252 + 34,531

→ P ' = 228,57   k N

Passo 5

Por fim, a gente calcula a pressão a mais em porcentagem, bora lá:

A u m e n t o   % = P ' - P W P W ⋅ 100 %

A u m e n t o   % = 228,57 - 213,66 213,66 ⋅ 100 %

A u m e n t o   % = 6,9874 %

Resposta

A u m e n t o   % = 6,9874 %

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A viga A B e 10m apoia, mas não está fixada, sobre aos suportes C e D . Desprezando o peso próprio da viga, determine o intervalo de valores de P para que a viga permaneça em equilibrio.
O máximo valor admissível de cada uma das reações é 180N . Desprezando o peso da viga, determine o intervalo de valores da distância d para a qual o apoio não se move.
Um trator de 9.450N é usado para erguer 4.050N de cascalho. Determine a reação em cada uma das duas (a) rodas traseiras A, (b) rodas dianteiras B.Figura P4.1
Para a viga e carregamento mostrados na figura, determine (a) a reação em A, (b) a tração no cabo BC.Figura P4.4
48. Para a viga e o carregamento mostrados na figura, determine o intervalo de valores de W para os quais a intensidade do binário em D não exceda a 54N ⋅ m .