Substitua a corrente do problema por uma corda flexível ou uma corrente de bibicleta de massa por unidade de comprimento e comprimento total . A extremidade livre é liberada a partir do repouso em e cai sob a influência da gravidade. Determine a aceleração da extremidade livre, a força na extremidade fixa e a tração na corda da curva, todas em termos de . (Note que é maior do que . O que acontece com a energia do sistema quando ?).
Figura do problema :
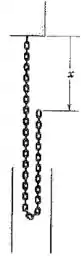
Passo 1
Primeiro queremos encontrar uma expressão para a aceleração em termos de .
Inicialmente, cada lado da corda (o que está preso e o que está livre) tem um comprimento . Conforme o lado livre cai por uma altura , o comprimento de cada lado vira:
Vamos pensar na energia mecânica da corda. A variação da energia cinética acontece porque a massa do lado solto ganha uma velocidade :
Agora vamos pensar na variação de energia potencial gravitacional, definido que o zero é a altura do teto.
Quando a massa do lado livre cai por uma altura , a variação de energia é:
E para essa mesma queda por uma altura , um pedaço de comprimento que “passa para o outro lado” durante o deslocamento dá:
E então:
Passo 2
Agora vamos aplicar a lei de conservação de energia:
E agora vamos isolar a velocidade:
Mas nosso objetivo é encontrar uma expressão para a aceleração em função do deslocamento, então vamos reescrever:
Para podermos aproveitar nosso resultado de cima com mais facilidade, vamos escrever o seguinte:
Então:
Passo 3
Então vamos usar a expressão que encontramos para para calcular essa derivada:
E precisamos usar a regra do quociente:
Passo 4
Agora vamos pensar nas forças que atuam sobre a corda. A soma das forças externas precisa ser igual à taxa de variação da quantidade de movimento:
Nesse caso as duas forças externas que agem sobre a corda (inteira) são o peso e a força na extremidade fixa:
E momento linear está associado à velocidade da parte livre da corda:
Pela regra do produto:
E agora substituindo tudo na primeira equação:
E vamos substituir nossas expressões para e para e isolar :
E essa é a expressão que estávamos procurando.
Passo 5
Agora queremos achar a tração na corda. O jeito mais fácil de encontrar essa expressão é considerar a parte fixa da corda. Já vimos que o seu peso é:
E a tração está apontando no mesmo sentido. Para que a parte fixa permanece em repouso essas duas forças precisam se igualar à força que acabamos de calcular:
Pronto!
Resposta
A força é , a tração é e a perda de energia é .