Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 4.7 - Ex. 87
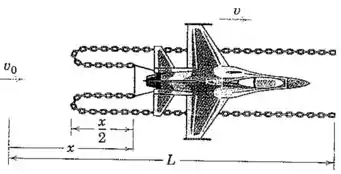
Na figura é apresentado um sistema utiliado para deter o movimento de um avião que pousa em um campo de comprimento restrito. O avião de massa se deslocando livremente com uma velocidade se prende a um gancho que puxa as extremidades de duas correntes pesadas, cada uma de comprimento e massa por unidade de comprimento, da forma indicada. Um cálculo conservativo da efetividade do dispositivo ignora a desaceleração causada pelo atrito da corrente no solo e qualquer outra resistência ao movimento do avião. Com essas hipóteses, calcule a velocidade do avião no instante em que o último elo de cada corrente é posto em movimento. Determine também a relação entre o deslocamento e o tempo após o contato com a corrente. Assuma que cada elo da corrente adquire sua velocidade subitamente no contato com os elos em movimento.
Passo 1
Vamos tratar o avião e a parte da corrente que está em movimento como se fosse um sistema só. Nesse caso, já que podemos desprezar todo tipo de atrito, não existe nenhuma força externa agindo sobre o sistema:
Mas a massa é variável, já que uma “quantidade” cada vez maior de corrente está em movimento. Vamos escrever uma expressão para essa massa:
Onde é a massa do avião e é a massa por unidade de comprimento da corrente. E a partir disso podemos encontrar o seguinte:
Além disso, a velocidade com que novos pedaços de corrente “entram no sistema” é igual a velocidade do avião, ou seja:
Então nossa equação fica:
Passo 2
Queremos encontrar a velocidade do avião no instante em que o último elo de cada corrente “entra” no sistema, então precisamos de uma função que dê a velocidade em função do tempo.
Podemos reescrever a nossa equação de cima do seguinte jeito:
Integrando:
Aplicando a exponencial sobre tudo isso:
E então a velocidade final é dada poro:
E olhando para a figura podemos ver que a velocidade que queremos calcular acontece quando :
Passo 3
A seguir queremos achar uma função para o deslocamento em função do tempo. Para isso precisamos reescrever da seguinte forma:
E integrando:
E podemos resolver essa equação do segundo grau para encontrar .
Passo 4
A equação é:
E aplicando a fórmula de Bhaskara:
Podemos colocar a razão em evidência:
Mas o enunciado pediu para chamarmos a massa do avião de , então vamos ajustar:
Resposta
A velocidade é e o deslocamento é .