Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.9 - Ex. 220
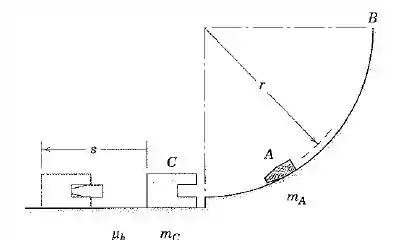
O tampão cilíndrico de massa é liberado a partir do repouso em e desliza para baixo na guia circular lisa. O tampão atinge o bloco e se encaixa nele. Escreva a expressão para a distância que o bloco e o tampão deslizam antes de atingir o repouso. O coeficiente de atrito dinâmico entre o bloco e a superfície horizontal é .
Passo 1
Bom galera, nesse exercício queremos encontrar a expressão para a distância . Pela conservação de energia, temos que
Dessa forma, temos
Isolando temos
Passo 2
Para a junta e o bloco, , Dessa forma, temos
A força de atrito pode ser dada por
Passo 3
Podemos então escrever
Sabendo que , temos
Resposta
Exercícios de Livros Relacionados
As duas esferas, cada uma com massa m , estão conectadas pela mola e barras articuladas de massa desprezível. As esferas estão livres para deslizar nas guias lisas subindo a inclinação θ . Determine a
As três pequenas esferas estão conectadas pelos cordões e pela mola e estão apoiadas em uma superfície horizontal lisa. Se uma força F = 6,4N é aplicada a um dos cordões, encontre a aceleração a - do
As três esferas idênticas de aço estão soldadas às duas barras de massa desprezível formando uma unidade rígida. O conjunto é liberado a partir do repouso na posição mostrada e desliza no plano vertic
As três barras idênticas, cada uma com massa de 8k g , são unidas pelos dois conectores livremente articulados de massa desprezível e estão em repouso sobre uma superfície horizontal lisa. Calcule a a
Calcule a aceleração do centro de massa do sistema de quatro cilindro de 10k g . Despreze o atrito e a massa das polias e cabos.