Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 4.5 - Ex. 10

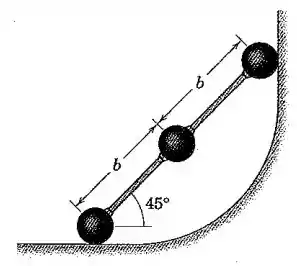
As três esferas idênticas de aço estão soldadas às duas barras de massa desprezível formando uma unidade rígida. O conjunto é liberado a partir do repouso na posição mostrada e desliza no plano vertical. Na ausência de atrito determine a velocidade em comum v das esferas quando elas atingem a superfície horizontal.

Passo 1

Como há conservação de energia no sistema, escrevemos:

Δ T + Δ V g = 0

No início, as esferas estão em repouso, e no final, todas têm velocidade v . Logo, a variação de energia cinética será:

Δ T = 1 2 3 m v 2 - 0

Δ T = 3 2 m v 2

Passo 2

Para o cálculo da variação da energia potencial gravitacional, consideramos a altura final (nível do chão) como zero, e então Δ V g será dada em função das alturas iniciais h 1 , h 2 e h 3 das esferas contadas a partir da esquerda para a direita:

Δ V g = 0 - m g h 1 + m g h 2 + m g h 3

Δ V g = - m g h 1 + h 2 + h 3

Porém, pela geometria da figura, temos:

h 1 = 0

h 2 = b   s e n   45 ° = b 2

h 3 = 2 b   s e n   45 ° = 2 b 2

Então:

Δ V g = - m g h 1 + h 2 + h 3 = - m g 0 + b 2 + 2 b 2

Δ V g = - 3 2 m g b

Passo 3

Substituindo as expressões obtidas na equação de conservação de energia, obtemos:

Δ T + Δ V g = 0

3 2 m v 2 - 3 2 m g b = 0

v 2 = 2 2 g b = 2 g b

v = g b 2

Resposta

v = g b 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um martelo de 650 kg de um bate-estaca cai de uma altura de 1,2 m sobre o topo de uma estaca de construção de 140 kg, movendo-se 110 mm no chão. Considerando um impacto plástico perfeito (e= 0), deter
Um ônibus espacial está indo de encontro a uma estação espacial que está em órbita circular a uma altitude de 400 km acima da Terra. O ônibus deve alcançar uma altitude de 60 km, quando seus motores s
Uma pequena esferaApresa a uma cordaACé liberada do repouso na posição mostrada na figura e atinge uma esfera idênticaBsuspensa pela corda verticalBD. Se o máximo ângulo θ B formado pela cordaBDcom a
Um blocoAde 2 kg é empurrado contra uma mola comprimindo a na distânciax= 0,1 m. O bloco é então liberado do repouso e desliza num declive de 20° até atingir uma esferaBde 1 kg que está suspensa por u
Os discosAeBcom massasmAemB, respectivamente, podem deslizar livremente em uma superfície horizontal sem atrito. O discoBestá em repouso quando é atingido pelo discoAque está em movimento com a veloci