Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 4.5 - Ex. 7

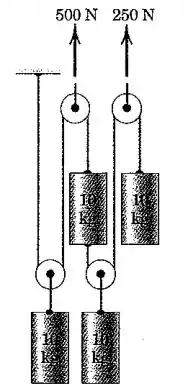
Calcule a aceleração do centro de massa do sistema de quatro cilindro de 10   k g . Despreze o atrito e a massa das polias e cabos.

Passo 1

Galera, as forças externas desse sistema de cilindros são os pesos de cada um, as forças indicadas de 500   N e 250   N , além da tração T no fio ligado ao teto. Essas forças estão mostradas no seguinte diagrama:

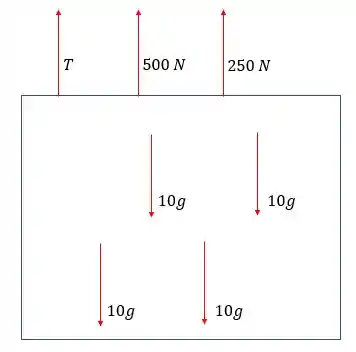
As outras forças de tração são internas ao sistema, e não precisaremos delas para o nosso cálculo.

Passo 2

Para descobrir o valor da tração T no fio que pende do teto, basta perceber que este é o mesmo fio que passa pela polia puxada por uma força de 500   N , então a tração nesse fio também é T . Como a polia não tem massa, as duas forças T em cada porção do fio devem totalizar 500   N , ou seja:

2   T = 500

T = 250   N

Agora estamos prontos para aplicar a Segunda Lei de Newton ao centro de massa:

∑ F = ∑ m i a -

T + 500 + 250 - 4 10 g = 4 10   a -

250 + 500 + 250 - 40 9,81 = 40   a -

  a - = 15,19   m / s 2

Resposta

  a - = 15,19   m / s 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma balança de mola A e uma balança de alavanca B com braços de alavanca iguais estão presas ao teto de um elevador e pacotes idênticos estão sendo segurados por elas, tal como mostra a figura. Sabend
O valor da aceleração da gravidade g em qualquer latitude ϕ pode ser dado pela fórmula g = 9,7087 1 + 0,0053sen 2 ϕ m/ s 2 onde o efeito da rotação da Terra e também o fato de que a Terra não ser esfé
Para transportar uma série de feixes de telhas A para um telhado, um empreiteiro usa um elevador motorizado que consiste em uma plataforma horizontal BC que se desloca em trilhos presos às laterais de
Para descarregar uma pilha de madeira compensada de um caminhão, o motorista primeiro inclina a carroceria do caminhão e depois acelera do repouso. Saber que os coeficientes de atrito entre a folha de
O bloco A tem uma massa de 40 kg e o bloco B tem uma massa de 8 kg. Os coeficientes de atrito entre todas as superfícies de contato são μ s = 0,20 e μ k = 0,15. Se P = 40 N -, determine (a) a aceleraç