Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.10 - Ex. 228
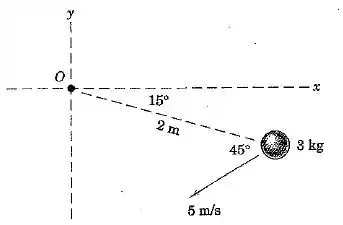
A esfera de se desloca no plano e tem a velocidade indicada em um determinado instante. Determine sua quantidade de movimento linear, quantidade de movimento angular em torno do ponto , e energia cinética.
Passo 1
Utilizando a definição de quantidade de movimento linear e os dados do problema, podemos encontrar a quantidade de movimento linear da esfera
Passo 2
Pela definição vetorial da quantidade de movimento angular, temos
Substituindo os valores do enunciado, temos o seguinte produto vetorial
Ao resolver o produto vetorial, encontramos então o valor da quantidade de movimento angular, que é
Passo 3
Podemos utilizar a definição de energia cinética para encontrar a energia cinética da esfera. Substituindo os valores dados, temos
Resposta
Exercícios de Livros Relacionados
Um pêndulo consiste em duas massas concentradas de 3,2k g posicionadas como mostrado em uma barra leve, porém rígida. O pêndulo está oscilando pela posição vertical com uma velocidade angular no senti
No ponto A de maior aproximação com o Sol, um cometa tem uma velocidade v A = 57,45 10 3 m / s . Determine as componentes radial e transversal de sua velocidade v B no ponto B, onde a distância radial
A partícula de 0,02k g se desloca ao longo da trajetória tracejada mostrada e tem as velocidades indicadas nas posições A e B . Calcule a média no tempo do momento em torno de O da força resultante P
As duas esferas de massas iguais m podem deslizar ao longo da haste horizontal que gira. Se elas estão inicialmente travadas na posição a uma distância r do eixo de rotação com o conjunto girando livr
Uma partícula é liberada na parede interna lisa de um reservatório cilíndrico em A com uma velocidade v 0 que faz um ângulo β com a tangente horizontal. Quando a partícula atinge um ponto B uma distân