Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 3.Problemas - Ex. 33
O tampão tem diâmetro de e ajusta-se ao interior de uma luva rígida com diâmetro interno de . Ambos, tampão e luva, têm de comprimento. Determine a pressão axial que deve ser aplicada à parte superior do tampão para que ele entre em contato com as laterais da luva. Determine também a que distância o tampão deve ser comprimido para baixo para que isso aconteça. O material do tampão tem
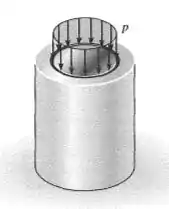
Passo 1
Queremos encontrar o valor da pressão axial (relativo ao eixo) , que vai fazer o papel de tensão normal, e também o quanto o tampão deve ser comprimido para baixo para que aconteça isso. Além disso, devemos lembrar que as deformações específicas podem ser consideradas em 2 formas longitudinais e latitudinais que obedecem as seguintes equações
Além disso, temos
Passo 2
Tendo as equações acima em mãos basta substituirmos os valores para encontrar , assim
Agora, aplicando a lei de Hooke vamos ter