Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 3.Problemas - Ex. 32
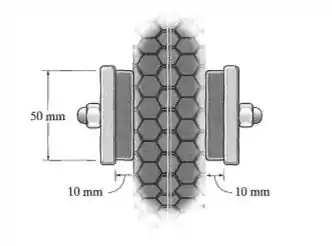
As sapatas do freio do pneu de uma bicicleta são feitas de borracha. Se uma força de atrito de for aplicada de cada lado dos pneus, determine a deformação por cisalhamento média na borracha. As dimensões da seção transversal de cada sapata são e .
Passo 1
E ai galera tudo bemm????
Então, o que ele quer dizer é que tem essas duas peças de borracha que seguram o pneu para que se alguma força tente fazer esse carinha rodar, ela não consiga.
E aí quem resiste a essa tendencia de movimento é a força de atrito, que é uma força paralela a seção da peça, que o enunciado diz ter dimensões . E já que é uma força paralela a seção da peça, ela gera tensão de cisalhamento nessa peça.
A ideia aqui é a gente olhar só para um lado do pneu mesmo e a seção de uma dessas peças, e ver a deformação da peça por causa da força de atrito entre o pneu e a peça que vale , tá bem?
Bora lá ver como achar essa deformação!
Passo 2
Antes de encontrarmos a deformação, vamos achar a tensão de cisalhamento média.
Vamos relembrar a equação dela:
Onde é a área da seção da peça paralela a força de atrito. E .
Substituindo nossas coisinhas aí:
Dica: sempre que a gente divide por o resultado sai em , beezinha?
Passo 3
Agora que encontramos a tensão de cisalhamento podemos encontrar a deformação por cisalhamento.
Isso porque o enunciado deu o valor do módulo de rigidez . Então podemos relacionar a tensão de cisalhamento e a deformação por cisalhamento através dessa expressão:
Isolando a deformação e substituindo nossos valores:
Isso vale para uma peça, certo? Portanto, a deformação por cisalhamento média em cada sapata é de .