Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 7.Problemas - Ex. 118
Para o tanque do problema , determine a maior pressão manométrica admissível, sabendo que a tensão normal perpendicular à solda é e a tensão de cisalhamento admissível paralela à solda é de
O tanque de pressão mostrado na figura tem uma parede com espessura de e possui emendas de solda de topo formando um ângulo com um plano transversal. Para uma pressão manométrica de , determine a tensão normal perpendicular à solda e a tensão de cisalhamento paralela à solda.
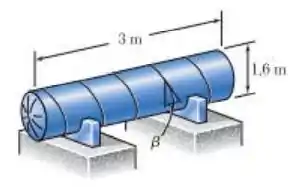
Passo 1
Fala aí, galera. Beleza? Bora pra mais um exercício.
Primeiramente, sabemos que a tensão normal para tubos de paredes finas sujeitos à pressão, é dada por:
Onde é a pressão interna, é o raio interno e é a espessura da parede. Além disso, a primeira pressão é a pressão na direção radial e a segunda é a pressão na direção axial.
Logo, sabemos que o raio interno é dado por:
Onde . Logo
Onde é a espessura de parede. Portanto, temos que a tensão média vai ser dada por:
Este vai ser o centro do círculo e, então, o raio do círculo de mohr vai ser:
Passo 2
Em seguida, para encontrarmos a menor pressão, temos que utilizara relação para a tensão normal perpendicular à solda. Ela é dada pelo raio do círculo de mohr, da tensão média e pelo cosseno de . Temos:
Onde . Logo, substituindo:
Isolando a pressão e substituindo, temos:
Passo 3
Por fim, vamos utilizar a tensão de cisalhamento paralela à solda para encontrarmos a menor tensão, temos:
Novamente, nosso vai ser . Portanto:
Substituindo :
Logo, a gente pode ver que a menor pressão é a primeira, portanto:
É isso, galera. Bora fazer mais questões.