Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 5.Problemas - Ex. 98
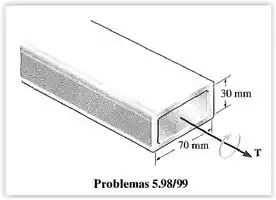
O tubo de aço inoxidável tem espessura de . Se a tensão de cisalhamento admissível for , determine o torque máximo que ele pode transmitir. Calcule também o ângulo de torção de uma extremidade do tubo em relação à outra se o tubo tiver de comprimento. Despreze as concentrações de tensão nos cantos. As dimensões médias são mostradas na figura.
Passo 1
Olá, galera!
O problema pede que determinemos torque máximo no tubo, se a tensão de cisalhamento admissível for e o ângulo de torção de uma extremidade do tubo em relação à outra. Ele nos fornece como dados:
Tubo de aço inoxidável , portanto, .
A tensão de cisalhamento em tubos de paredes finas é determinada levando-se em conta o fluxo de cisalhamento no tubo e é considerada constante em cada espessura . Sua fómula é dada por:
A partir dela podemos calcular o torque aplicado ao tubo. A área média contida no contorno da linha central da espessura do tubo, , vamos encontrar usando as medidas fornecidas na figura.
Passo 2
Substituindo os valores na fómula da tensão de cisalhamento média, temos:
Passo 3
Agora vamos descobrir o ângulo de torção de uma extremidade do tubo em relação à outra.
O ângulo de torção, , provocado pelo torque, , é determinado pela seguinte equação:
Em que representa o comprimento em torno da linha central do contorno do tubo. Podemos então calcular fazendo:
Substituindo valores na equação, temos:
Convertendo para graus: