Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 3.Problemas Revisão - Ex. 140

Dois eixo maciços de aço são acoplados pelos flanges em B e engastados a suportes rígidos em A e C. Para o torque mostrado, determinar a máxima tensão de cisalhamento (a) no eixo AB (b) no eixo BC.

Passo 1

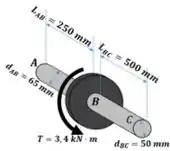
Esta é uma questão estaticamente indeterminada. Isso quer dizer duas coisas

  1. A soma do torque nos eixos AB e BC é igual ao torque aplicado:

    2. T A B + T B C = 3,4   k N m

  2. O ângulo de torção no ponto B é igual para os dois eixos:

ϕ A B = ϕ B C

Passo 2

Vamos expandir a igualdade dos ângulos:

ϕ A B = ϕ B C

Aplicamos a equação do ângulo de torção nos dois lados:

T A B L A B J A B G = T B C L B C J B C G

Podemos simplificar o G dos dois lados, e expandir o momento de inércia polar

T A B L A B π d A B 4 / 32 = T B C L B C π d B C 4 / 32

Vamos isolar T A B

T A B = T B C L B C d A B 4 d B C 4 L A B

E aplicamos os valores:

T A B = T B C 500   m m ⋅ 65   m m 4 50   m m 4 ⋅ 250   m m

Chegamos em uma relação entre os torques.

T A B = 5,71 ⋅ T B C

Passo 3

Para encontrar os torques vamos resolver o sistema

T A B + T B C = 3,4   k N m T A B = 5,71 ⋅ T B C

Resolvendo esse sistema, o resultado é:

T A B = 2,493   k N ⋅ m

T B C = 0,507   k N ⋅ m

Passo 4

Agora vamos calcular a tensão no eixo AB: τ A B = T C D c C D J

τ A B = T ⋅ d 2 π d 4 32

τ A B = 3,4   k N m ⋅ 65   m m 2 π ⋅ 65   m m 4 32

τ A B = 63,05   M P a

Passo 5

E terminamos a questão calculando a tensão no eixo BC: τ B C = T B C c B C J B C

τ B C = T B C ⋅ d B C 2 π d B C 4 32

τ B C = 3,4   k N m ⋅ 50 m m 2 π ⋅ 5 0   m m 4 32

τ B C = 138,53   M P a

Resposta

τ A B = 63,05   M P a

τ B C = 138,53   M P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para o tanque de ar comprimido do Problema 7.112 , determine a pressão manométrica que provocará uma tensão de cisalhamento paralela à solda de 30M P a .A parte cilíndrica do tanque de ar comprimido m
Determine a maior pressão interna que pode ser aplicada a um tanque cilíndrico com 55,5p é s é de diâmetro externo e 5 8 i n de espessura de parede, se o limite de tensão do aço utilizado é de 65k s i
Uma adutora de aço tem diâmetro externo de 36i n , uma espessura de parede 0,5i n e conecta um reservatório em A com uma estação geradora de energia em B . Sabendo que a densidade da água é de 62,4l b
A parte cilíndrica do tanque de ar comprimido mostrado na figura é fabricada com uma placa de 8m m de espessura soldada ao longo de uma hélice formando um ângulo β = 30 ° com a horizontal. Sabendo que
Um vaso de pressão com diâmetro interno de 254m m , espessura de 6,35 m m e comprimento de 1219m m é soldado em espiral e possui duas tampas laterais rígidas. A pressão manométrica dentro do vaso é de