Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 3.Problemas Revisão - Ex. 135
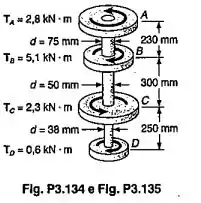
Os torques mostrados são aplicados às polias A, B, C e D. Sabendo-se que cada trecho do eixo é maciço e são feitos de aço, com G=77GPa, determinar o ângulo de torção da polia C, em relação a (a) polia A (b) polia D
Passo 1
No exercício 134 a gente calculou as forças que atuam em cada seção do eixo:
Para calcular os ângulos de torção vamos usar a fórmula:
Se a gente aplicar a equação do momento de inércia polar teremos:
Passo 2
Nós já temos todas as informações necessárias para calcular as deformações de cada seção.
O ângulo de torção na seção AB é:
Na seção BC é:
Na seção CD a torção é igual a zero, então o ângulo de torção também é zero:
Passo 3
Como a torção na seção é nula, então a deformação em C em relação a D será:
Passo 4
A deformação em BC é em sentido anti-horário a deformação em AB é em sentido horário. Então, a deformação de C em relação a A será.