Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 1.Problemas - Ex. 100
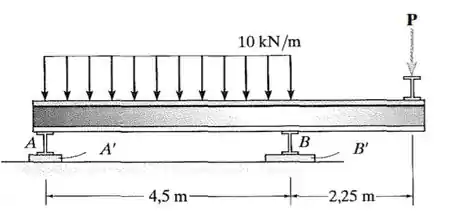
Se a tensão de apoio admissível para o material sob os apoios em e for , determine a carga máxima que pode ser aplicada à viga. As seções transversais quadradas das chapas de apoio e são e , respectivamente.
Passo 1
Falaaa! Queremos descobrir o valor máximo da carga que pode ser aplicada à viga, tendo a tensão normal máxima admissível e as dimensões das chapas de suporte para e .
Primeiramente, vamos escrever em função de as reações de suporte.
Adotando o sentido anti-horário como positivo e lembrando que a carga distribuída pode se concentrar no meio desses tendo módulo
vamos ter
Pelo somatório de forças em :
Passo 2
Aí a gente vai lembrar que a tensão normal é dada por
Então a gente pode compara esse valor de tensão média com o de tensão admissível.
Sendo a força vertical que atua em cada caso. E repara que nossas reações de apoio são exatamente essa força vertical para e . Além disso, como temos que as chapas são quadradas podemos escrever.
Assim, para cada um dos casos vamos ter
Isolando :
Para o segundo caso vamos ter
Nosso valor de máximo vai ser o mínimo valor entre os valores de encontrados para cada caso. Portanto, devemos ter