A viga composta de madeira está interligada por um parafuso em . Considerando que os acoplamentos em exerçam somente forças verticais na viga, determine o diâmetro exigido para o parafuso em e o diâmetro externo exigido para as respectivas arruelas se a tensão de tração admissível para o parafuso for e a tensão de apoio admissível para a madeira for . Considere que o orifício das arruelas tem o mesmo diâmetro do parafuso.

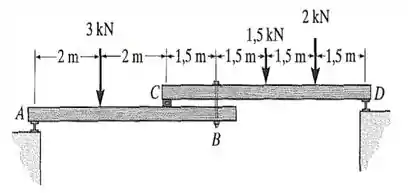
Desejamos encontrar o valor do diâmetro para o parafuso em e o diâmetro externo exigido para as arruelas. Para isso, calculemos primeiramente os momentos em e em (adotando o sentido anti-horário como positivo) para obtermos as forças que nos servirão de base para encontrarmos os diâmetros. Assim

Resolvendo o sistema para obtemos