Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 1.Problemas - Ex. 97
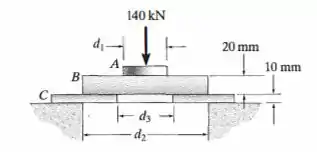
O conjunto consiste em três discos usados para suportar a carga de . Determine o menor diâmetro do disco superior, o diâmetro do espaço entre os apoios e o diâmetro do orifício no disco inferior. A tensão de apoio admissível para o material é e a tensão de cisalhamento admissível é .
Passo 1
Fala aí bonitões, como é que vocês estão, tudo certo por aí? Espero que sim.
Vamos lá meu povo, pensar nesse probleminha aqui: nós queremos encontrar as dimensões dos diâmetros indicados na figura e, para isso, devemos relacionar esses valores com os valores de tensão normal/cisalhamento admissíveis já que esses dados não foram fornecidos no enunciado de graça, não acha?
Pois bem, para isso vamos utilizar as equações dessas tensões mesmos. Essas equações são
Analogamente para a tensão normal nós teremos
Passo 2
Já que a gente tem os valores das tensões admissíveis vamos observar os discos e vamos assumir falha por cisalhamento, a começar pelo disco de tal forma que obteremos
Nossa área será a área lateral de um cilindro dada por
Assim, teremos
Já que estamos no disco vamos continuar nele só que agora vamos supormos uma falha no rolamento desse disco e assim teremos
Nesse caso nossa área vai ser uma coroa circular com raio externo e raio interno , logo a área vai ser dada fazendo
Dessa forma, teremos
Passo 3
Agora é só partir pro abraço, porque o exercício está praticamente finalizado, mas a gente ainda precisa terminar, né? Então vamos lá
Para encontrarmos o diâmetro 1 vamos supor uma falha como a anterior, só que agora para o disco , dessa forma vamos ter
Pronto, acabou esse problema.