Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 3.Problemas - Ex. 56
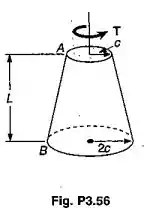
Um torque é aplicado como mostrado a um tronco de cone maciço AB. Mostrar por integração que o ângulo de torção em A é:
Passo 1
Para facilitar tudo, vamos desenhar um prolongamento no nosso tronco de cone:
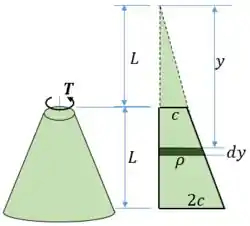
Primeiro vamos definir o momento de inércia polar. Para isso, vamos considerar a seção qualquer (destacada em verde escuro) de raio e espessura . O momento de inércia polar em função de será:
E por semelhança de triângulos, podemos definir em função de
Aplicando no momento de inércia polar:
Passo 2
Podemos dizer que o ângulo de torção é dado por:
Aplicando o valor do momento de inércia:
Reorganizando:
Passo 3
Agora a hora favorita da galera: HORA DA INTEGRAÇÃO
Vamos lá. Aqui basta ter cuidado com os limites de integração. Lá no Passo 1, a gente completou o troco de cone para fazer um triângulo. Isso quer dizer que o nosso limite de integração não deve começar em , mas sim em e variar até
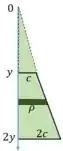
Mas não se preocupe, que dá para resolver a integral com tranquilidade.
Primeiro colocamos as constantes para fora:
E trocamos
E aplicamos a integração dos dois lados:
Aplicamos os limites:
Vamos fazer um pouco de álgebra
Chegamos na resposta: