Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 5.Problemas - Ex. 52
O parafuso de aço A-36 com 8 mm de diâmetro está parafusado firmemente ao bloco em A. Determine as forças conjugadas F que devem ser aplicadas à chave de torque de modo que a tensão de cisalhamento máxima no parafuso seja de 18 MPa. Calcule também o deslocamento correspondente de cada força F necessário para causar essa tensão. Considere que a chave de torque seja rígida.
Passo 1
Oláaaa, querido! Cê tá bem?
Então, temos um eixo (no caso, o parafuso), que sofre uma torção por causa desse par de forças . Aí essa torção gera uma tensão de cisalhamento no parafuso e também causa nele um ângulo de deformação.
Antes de colocarmos a mão na massa, vamos listar os dados que nós temos e quem queremos encontrar:
Aço A-36, portanto,
Aí o que ele quer é saber o valor da força para que a tensão de cisalhamento no parafuso seja a máxima de . E quer saber também o deslocamento da força para que essa tensão aconteça. Como assim?
Bem, a tensão causa uma deformação no parafuso, aí o deslocamento do ponto de aplicação da força é resultado dessa deformação. Como a tensão é causada por , podemos ver qual é o deslocamento que tem, se ela causa .
Agora que gente fez essa visão geral e listou alguns dados, vamos partir para achar o que ele pede? Bora!
Passo 2
Inicialmente, vamos encontrar o valor da torção que precisa ser causada pelas forças para que . E vamos fazer isso utilizando a formulinha da para a torção máxima:
A torção máxima ocorre no ponto mais distante do centro da seção, ou seja, quando é igual ao raio da seção:
E como queremos :
Já é o nosso momento polar de inércia, e que é dado por:
Com . Jogando isso na fórmula da torção:
Atribuindo valores à fórmula, temos:
Passo 3
Beleza, encontramos o valor de agora. Bora fazer um DCL para visualizar o torque interno no parafuso
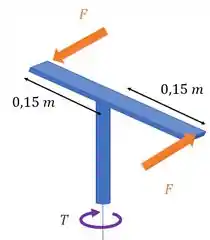
Aí pelo equilíbrio de momentos nesse eixo vertical:
Simplificando e substituindo o valor de
Isolando
Passo 4
Falta achar o deslocamento do ponto de aplicação da força , né? Vamos refletir aqui. A deformação que o parafuso sofre com a torção causa essa deformação nele:
Ou seja, a extremidade do parafuso sofre uma deformação angular . Por isso, essa haste de cima vai rotacionar , e assim o ponto de aplicação de se desloca . Para achar , precisamos descobrir o nosso ângulo de torção
Ele tem essa fórmulinha:
Atribuindo valores a fórmula:
Passo 5
Estamos quase matando a questão. Percebe que na nossa figura é a aproximadamente o comprimento de arco do setor que tem raio e ângulo de abertura , já que é bem pequeno. Então podemos dizer que:
Onde é a distância da força até o parafuso. 😉 Substituindo os valores:
Executamos mais uma! VAPO!
