Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 5.Problemas - Ex. 51
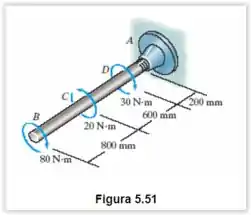
O eixo de aço A-36 de de diâmetro é submetido aos torques mostrados. Determine o ângulo de torção da extremidade .
Passo 1
Oi, pessoal! Tudo bem com vocês? O nosso problema pede que determinemos ângulo de torção da extremidade , e para isso nos fornece:
Aço A-36, portanto,
Vamos, inicialmente, fazer o diagrama de corpo, para que possamos determinar os torques em cada seção.
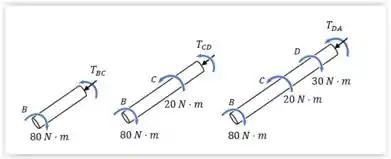
Cortando uma seção através do eixo e fazendo o somatório do momento, temos:
Agora cortando uma seção através do eixo :
Agora cortando uma seção através do eixo :
Passo 2
O ângulo de torção na extremidade , é dado por:
Para calcular o ângulo, utilizamos a equação:
O momento polar de inércia, , é dado por:
O diâmetro e o material do eixo é o mesmo em todas as seções, então para encontrar , temos:
Passo 3
Agora substituindo os valores na equação, lembrando de dividir o diâmetro por 2 para obter o raio , temos:
Convertendo para graus: