Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 7ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 7º - Capítulo 4.Problemas - Ex. 28
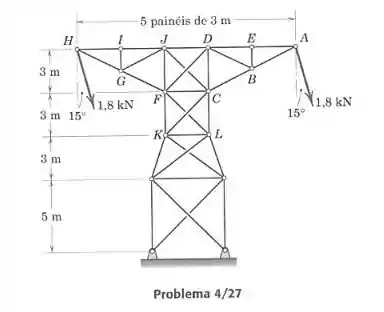
A torre para uma linha de transmissão é modelada pela treliça mostrada. Pode-se considerar que os elementos cruzados nas seções centrais da treliça somente suportam tração. Calcule as forlças induzidas nos elementos , e , para as cargas de 1,8 kN aplicadas no plano vertical.
Passo 1
Vamos calcular as forças pelo método dos nós, aplicando as equações de equilíbrio no eixo e no eixo para cada nó, começando por . Aqui não vamos calcular as equações de equilíbrio para as forças externas da treliça porque só queremos resolver as equações para algumas barras que estão bem longe das forças desconhecidas nos apoios. T significa que a força é de tração na barra, e C significa que é de compressão. Nas equações sempre consideraremos as forças como se fossem de tração e se o valor for negativo quer dizer que é de compressão.
Passo 2
Nó A:
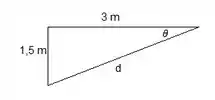
Precisamos do ângulo de inclinação da barra para calcular as equações:
Passo 3
Nó E:
Como pode ser considerado como uma barra só:
Passo 4
Nó B:
Como , se causar alguma compressão ou tração, haverá uma componente perpendicular a e que não poderá ser anulada por nenhuma força. Logo:
Além disso:
Passo 5
Não temos informações suficientes para calcular a equação no nó e encontrar . Vamos então ao outro lado da treliça calcular as equações da esquerda pra direita.
Nó H:
Passo 6
Agora acontecerá o mesmo que no lado direito da treliça. e poderão ser considerados como um elemento só, então:
Eliminando as barras inúteis do problema, ficamos com o seguinte desenho:
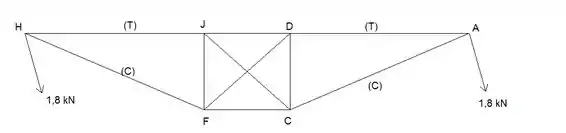
Uma das duas barras diagonais será de compressão e deverá ser ignorada. Se as diagonais não existissem seria tracionada. Então:
Como é perpendicular às barras horizontais de cima e não há outras forças com componente vertical em , a força nessa barra deve ser zero também.
é então uma barra só:
Passo 7
Agora podemos ir para o nó D:
Nó D: