Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 7ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 7º - Capítulo 4.Problemas - Ex. 8
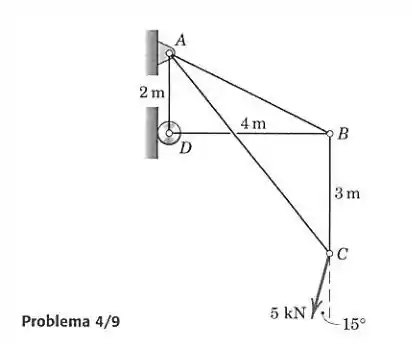
Determine a força em cada elemento da treliça carregada.
Passo 1
Vamos calcular as forças pelo método dos nós, isolando cada pino da treliça. Primeiro vamos às equações externas da treliça, para acharmos os valores de reação de e . Note que o apoio em só causa reação para a direita:
Obtemos calculando o momento em torno de :
Agora obtemos :
Uma coisa que devemos perceber para resolver a questão é que o elemento não está sob efeito de nenhuma força. Isso acontece porque não existe em nada que possa anular uma força vertical feita por .
Passo 2
Analisando o triângulo , calculamos o tamanho por Pitágoras:
Então temos o seno e o cosseno do ângulo entre e :
Agora, se colocarmos um ponto abaixo de e na mesma altura que , temos o triângulo retângulo , com e . Fazendo Pitágoras nele achamos o tamanho :
Podemos agora achar o seno e o cosseno do ângulo entre e :
Passo 3
Agora vamos calcular as equações para cada nó. indica que o elemento está comprimido e indica que ele está tracionado. Consideraremos todas as forças desconhecidas de tração, e se obtivermos um valor negativo quer dizer que são de compressão
Nó D:
Passo 4
Nó B:
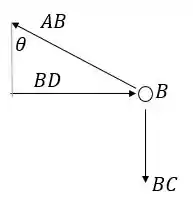
Passo 5
Nó C:
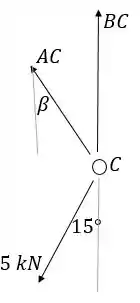
Substituindo os valores dos senos, finalmente encontramos: