Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 5.Problemas - Ex. 60

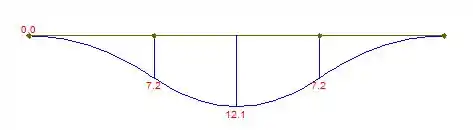
Trace os diagramas de força cortante e momento fletor para a viga e carregamento mostrados e, determine a tensão normal máxima provocada pelo momento fletor.

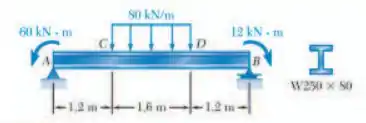
Passo 1

Fala aí, galerinha. Tudo bem com vocês? Bora estudar mecânica e garantir aquele notão na prova.

Como queremos a tensão normal máxima gerada pelo momento fletor, devemos, primeiramente, traçar o diagrama do momento fletor e, assim, identificar o seu ponto de máximo .   Para isso, precisamos determinar as reações e encontrar o diagrama. O DCL é dado por:

Para acharmos as reações, vamos utilizar as equações de equilíbrio. Sabemos que:

∑ M B = 0 → 60 - 12 + 80 1,6 2 - 4 F A = 0

F A = 76   k N

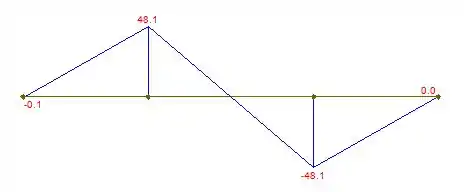
Portanto, podemos esboçar o diagrama de força cortante. Fazendo ele:

E também, o diagrama de momento:

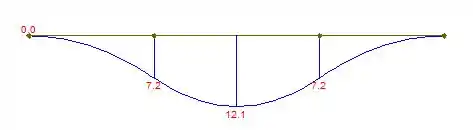
Com os diagramas traçados, podemos ver que o momento fletor máximo:

M m á x = 12,1   k N ∙ m

Agora, vamos determinar a tensão .

Passo 2

Já temos o momento máximo ,   agora basta encontrar as outras variáveis das quais a tensão normal depende. Sabemos que a tensão normal causada pelo momento fletor é dada por:

σ m á x = M m á x W

Onde W   é o valor mínimo admissível do módulo de resistência da seção da viga. Esse valor é tabelado para o perfil indicado, que é o W 200 × 22 , 5 e pode ser encontrado em tabelas na internet ou no próprio livro. Assim:

W = 193 × 10 - 6   m 3

Passo 3

Agora, temos todos os dados para obter a tensão normal .   Substituindo os valores:

σ m á x = M m á x W

σ m á x = 12,1 × 10 3 193 × 10 - 6 σ m á x = 6 2 , 2   M P a

E pronto! Esta é a tensão normal máxima   gerada pelo momento fletor.

Resposta

Cortante:

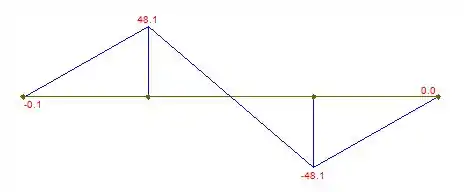
Momento:

σ m á x = 62,2   M P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um momento de 7,5k N m é aplicado ao perfil de aço laminado S 310 x 74 mostrado. Pede-se:Sendo que o momento encurva a viga em torno de um eixo horizontal, determinar a máxima tensão e o raio de curva
Determinar as equações das curvas dos diagramas de força cortante e de momento fletor para a viga com o carregamento mostrado e determinar também o máximo valor absoluto,
Determinar as equações das curvas dos diagramas de força cortante e de momento fletor para a viga com o carregamento mostrado. Determinar também o máximo valor absoluto fletor na viga.
Determinar as equações das curvas dos diagramas de força cortante e de momento fletor para a viga com o carregamento mostrado. Determinar também o máximo valor absoluto fletor na viga.
Uma viga A B é um sólido de revolução de diâmetro variável d . Para a porção A C da viga, expressar d , em termos de d 0 ,x e L , sabendo-se que a viga deve ser de igual resistência quando suporta o c