Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 6.Problemas - Ex. 76
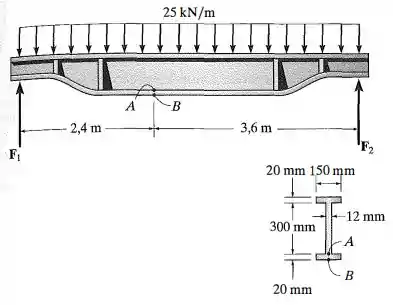
A travessa ou longarina de suporte principal da carroceda do caminhão está sujeita à carga distribuída uniforme. Determine a tensão de flexão nos pontos e .
Passo 1
Fala aí pessoal, vamos para mais um exercício de resmat. Primeiro, vamos determinar o DCL:
Para cada trecho, vamos calcular a carga resultante e colocar no centro do vão usando:
Assim:
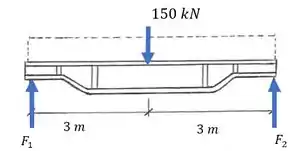
Também iremos fazer o mesmo processo para a seção que vai da extremidade esquerda até o a linha aonde estão os pontos que queremos avaliar.
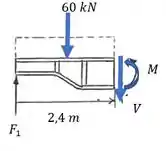
Passo 2
Em seguida, podemos encontrar o valor da força , pois sabemos que pela condição de simetria , logo, pela condição de equilíbrio no eixo , vamos encontrar . Temos:
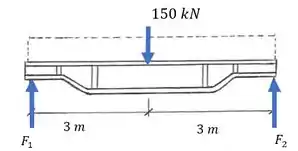
E então, vamos encontrar o momento, olhando para a nossa seção:
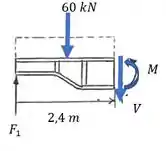
Considerando o sentido anti-horário como positivo, vamos calcular o momento na extremidade direita da nossa seção:
Passo 3
Com isso, podemos calcular o momento de inércia e precisaremos separar a figura pra facilitar os nossos cálculos:
As duas abas da mesa estão afastadas do centro, usando o teorema dos eixos paralelos o momento de inércia delas será:
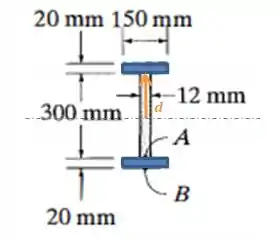
Onde , e d, pelo teorema dos eixos paralelos é a distância do centro da seção até o centro da mesa, em y que dá .
Assim:
E o momento de inércia da alma pode ser dado por:
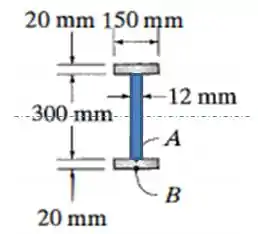
Onde:
Por fim, basta encontrarmos as tensões nos pontos e . Para , temos:
Onde é a distância do centro até o ponto A e mede 0,15m.
E para , temos:
Onde é a distância do centro até o ponto B e mede 0,17m.