Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 4.Problemas - Ex. 72
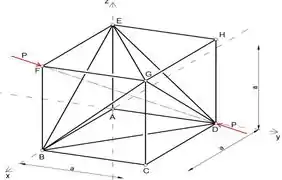
Uma treliça espacial é construída na forma de um cubo com seis membros diagonais mostrados. Verifique se a treliça está internamente estável. Se a treliça está sujeita às forças compressivas P
Passo 1
Verificaremos se a treliça é estaticamente determinada internamente pela equação abaixo
Onde m é um número de membros e j número de juntas. Esta treliça contém seis juntas e doze membros
Uma vez que a equação é satisfeita, isso significa que a treliça é determinada estaticamente
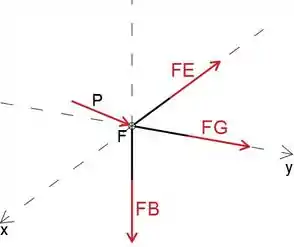
Podemos ver que existem três forças desconhecidas agindo no ponto F, portanto, analisando a junta F, podemos determinar as forças EF e FG
Passo 2
Vamos supor que todos os membros estejam em tensão
Podemos ver que as forças FE, FG e FB são paralelas aos eixos x, y, z, respectivamente, para que possamos escrevê-los como
Passo 3
Podemos escrever o vetor força P ⃗ como um produto de sua magnitude P e um vetor unitário de direção da força
Podemos ver na imagem que as coordenadas dos pontos F e D são
Uma vez que conhecemos dois pontos na linha de ação, podemos escrever nP como
Passo 4
Agora que escrevemos todas as forças como vetores, podemos escrever três equações de equilíbrio igualando a soma das forças a zero
Agora temos 3 equações de equilíbrio
(1)
(2)
(3)
Passo 5
Da equação (1), podemos determinar a força no membro EF
Obtivemos um resultado negativo, o que significa que o membro EF está em compressão
Da equação (2), podemos determinar a força no membro FG
Ao analisar a junta H e igualar a soma das forças na direção x a zero, fica claro que a força no membro GH é igual a zero
Ao analisar a junta C e igualar a soma das forças na direção z a zero, fica claro que a força no membro CG é igual a zero
Passo 6
Agora, existem três forças desconhecidas agindo no ponto G, então, analisando a junta G, podemos determinar a força no membro EG
Vamos assumir que todos os membros estão em tensão e como sabemos que os membros EG, BG e DG são diagonais de quadrados que se encontram nos planos xOy, xOz e yOz respectivamente, podemos escrevê-los como
Agora que escrevemos todas as forças como vetores, podemos escrever três equações de equilíbrio igualando a soma das forças a zero
Agora temos 3 equações para o equilíbrio
(4)
(5)
(6)
Passo 7
Vamos multiplicar a equação (6) por (-1)
(7)
Agora, adicionando as equações (4), (5) e (7), obteremos a equação em que EG é a única incógnita