Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 4.3 - Ex. 18

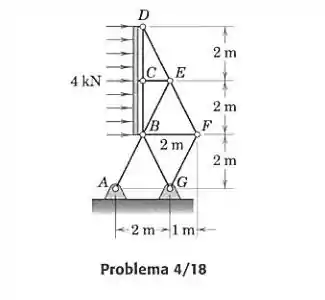
A treliça da placa de sinalização é projetada para suportar uma carga horizontal de 4 kN devida ao vento. Uma análise separada mostra que 5/8 dessa força são transmitidos para o nó central em C e o restante é dividido igualmente entre D e B . Calcule as forças nos elementos B E e B C .

Passo 1

Primeiro devemos analisar as força externas que atuam na treliça. Calculando as forças causadas pelo vento, temos em C a força para a direita:

C = 4 ⋅ 5 8 = 2,50   k N

E em D e B as forças iguais a:

B = D = 4 ⋅ 3 8 2 = 0,750   k N

Passo 2

Agora, vamos resolver as equações de equilíbrio em x e y   para cada nó, começando de cima. As forças positivas indicam tração e as negativas compressão, e sempre trataremos as forças desconhecidas como tração. Todas as barras inclinadas têm o mesmo ângulo θ com a horizontal. Vamos calcular o seno e o cosseno desse ângulo:

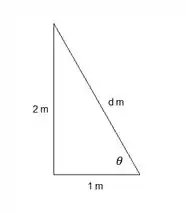
Por Pitágoras achamos d :

d 2 = 2 2 + 1 2 = 5 ⇒ d = 5

Então:

sen ⁡ θ = 2 5

cos ⁡ θ = 1 5

Passo 3

Nó D:

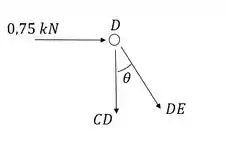
Para o eixo x :

∑ F x = 0 ⇒ D + D E cos ⁡ θ = 0 ⇒ D E = - D cos ⁡ θ

Agora substituindo pelo valor de cos ⁡ θ encontrado:

D E = - 0,75 1 5 = - 0,75 5 = - 1,68   k N   ( C )

Agora para o eixo y :

∑ F y = 0 ⇒ - C D - D E sen ⁡ θ = 0 ⇒ C D = - D E sen ⁡ θ

⇒ C D = - - 0,75 5 ⋅ 2 5 = 1,50   k N   ( T )

Passo 4

Nó C:

∑ F x = 0 ⇒ C + C E = 0 ⇒ C E = - 2,50   k N   ( C )

∑ F y = 0 ⇒ C D - B C = 0 ⇒ B C = 1,50   k N   ( T )

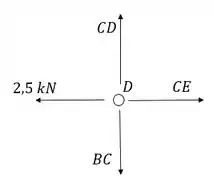
Passo 5

Nó E:

∑ F x = 0 ⇒ - D E cos ⁡ θ - C E - B E cos ⁡ θ + E F cos ⁡ θ = 0

⇒ - - 0,75 5 ⋅ 1 5 - - 2,5 - B E 5 + E F 5 = 0

⇒ B E - E F = 3,25 5

∑ F y = 0 ⇒ D E sen ⁡ θ - B E sen ⁡ θ - E F sen ⁡ θ = 0

⇒ - 0,75 5 ⋅ 1 5 - 2 B E 5 - 2 E F 5 = 0

⇒ B E + E F = - 0,375 5

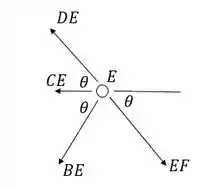
Resolvendo, achamos: (somando)

2 B E = 3,25 5 + - 0,375 5

B E = 3,21   k N

Resposta

B C = 1,50   k N   ( T )

B E = 3,21   k N   ( T )

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

59. Uma treliça de telhado tipo Polinésia ou dupla inclinação é carregada como mostrado na figura. Determine a força nos elementos, D F ,E F e E G .
60. Uma treliça de telhado tipo Polinésia ou dupla inclinação é carregada como mostrado na figura. Determine a força nos elementos, H I ,G I e G J .
42. A treliça mostrada na figura consiste em 18 elementos e é sustentada por uma rótula em A , duas pequenas hastes de conexão em B e uma pequena haste de conexão em G . ( a ) Verifique se essa treliç
39. A treliça mostrada na figura consiste em nove elementos e é sustentada por uma rótula em B , uma pequena haste de conexão em C e por duas pequenas hastes em D . ( a ) Verifique se essa treliça é u
40. Resolva o Problema 6.39 para P = 0 e Q = - 900N k