Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.10 - Ex. 181
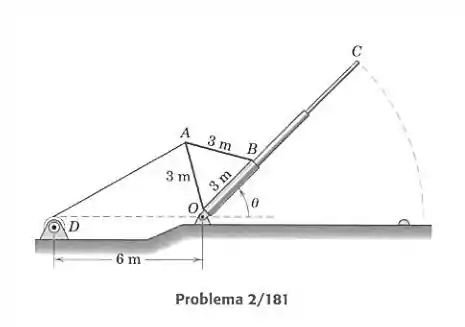
Um mastro de uma bandeira com uma estrutura triangular leve está mostrado aqui em uma posição arbitrária durante sua elevação. A força trativa de 75 N no cabo de elevação se mantém constante. Determine, e mostre em um gráfico, o momento em relação a da força de 75 N para a faixa . Determine o valor máximo deste momento e o ângulo de elevação no qual ele ocorre; comente a relevância física deste último valor. Os efeitos do diâmetro do carretel em podem ser ignorados.
Passo 1
Para obtermos a expressão vetorial da tração e assim conseguirmos calcular o momento em relação a , precisamos primeiro definir a posição do ponto em função do ângulo . O ponto percorre um círculo de raio igual a 3 m em volta do ponto , com o ângulo entre e (definindo como horizontal para a direita) sendo igual a . Então as coordenadas de são:
Passo 2
Agora que sabemos a posição de , podemos obter o vetor unitário que tem a mesma direção que a força . Vamos então calcular , sendo o módulo do vetor :
Então:
Passo 3
Como nossa força tem um módulo constante igual a 75 N e a direção dada por , então podemos escrevê-la assim:
Podemos então calcular nosso momento , aplicando o produto vetorial :
Passo 4
A próxima figura mostra um gráfico de em função de :
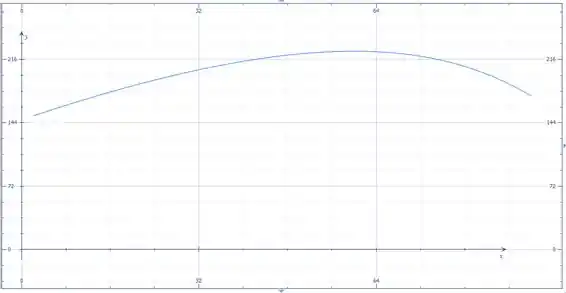
Analisando o gráfico encontramos um máximo quando .