Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 4.3 - Ex. 7

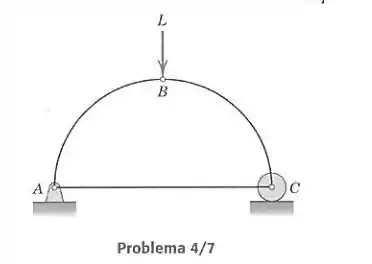
Determine a força no elemento A C da treliça carregada. Os dois elementos com formato de ¼ de círculo atuam como elementos de duas forças.

Passo 1

Vamos calcular as forças pelo método dos nós, isolando cada pino da treliça. Primeiro vamos às equações externas da treliça, para acharmos os valores de reação de A e C . Note que o apoio em C só causa uma reação para cima. Sendo r o raio do círculo:

∑ F x = 0 ⇒ A x = 0

∑ F y = 0 ⇒ A y + C y - L = 0 ⇒ A y = L - C y

∑ M A = 0 ⇒ - L r + C y 2 r = 0 ⇒ r L = 2 r C y ⇒ C y = L 2   ( p a r a   c i m a )

⇒ A y = L - L 2 = L 2   ( p a r a   c i m a )

Passo 2

Agora vamos calcular as equações para cada nó. C indica que a barra está comprimida e T indica que ela está tracionada. Os arcos A B e B C atuam como se fossem barras retilíneas, inclinadas com ângulo em relação à horizontal de 45 ° .

Nó A:

O elemento A B está certamente comprimido, então vamos às equações de equilíbrio:

∑ F y = 0 ⇒ - A B sen ⁡ 45 ° + A y = 0 ⇒ 2 2 A B = L 2 ⇒ A B = L 2   ( C )

∑ F x = 0 ⇒ - A B cos ⁡ 45 ° + A C = 0 ⇒ A C = L 2 ⋅ 2 2 ⇒ A C = L 2   ( T )

Passo 3

Nó B:

∑ F y = 0 ⇒ A B sen ⁡ 45 ° + B C sen ⁡ 45 ° - L = 0

⇒ 2 2 ⋅ L 2 + 2 2 B C - L = 0

⇒ 2 2 B C = L - L 2 = L 2 ⇒ B C = L 2   ( C )

Resposta

A B = L 2   ( C )

A C = L 2   ( T )

B C = L 2   ( C )

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A treliça espacial é sustentada por uma junta esférica em D e ligações curtas em C e E . Determine a força em cada membro e indique se os membros estão sob tração ou compressão. Considere F 1 = 200 i
O mecanismo de duas barras consiste de uma alavanca A B e uma barra lisa C D , que possui um colar liso fixo em sua extremidade C e um rolete na outra ponta D . Determine a força P necessária para man
Determine as componentes horizontal e vertical da reação que os pinos A e B exercem sobre a estrutura de dois membros. Faça F = 0 .
Determine as componentes horizontal e vertical da reação nos apoios pinados A e E da montagem de vigas compostas.
Determine as componentes horizontal e vertical da reação que os pinos A e B exercem sobre a estrutura de dois membros. Faça F = 50 0N .