Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 13.Problemas - Ex. 3
O trem de Mg parte do repolso e começa a subir o aclive, como mostrado. Se o motor exerce uma força de tração de do peso do trem, determine a velocidade do trem quando ele tiver avançado uma distância de km aclive acima. Despreze a resistência ao rolamento.
Passo 1
A primeira etapa de solução do problema é aplicar o diagrama de corpo livre no sistema para obtermos a equação do movimento.
Sabendo que as direções dos eixos e são representadas, respectivamente, pelos valores e , temos:
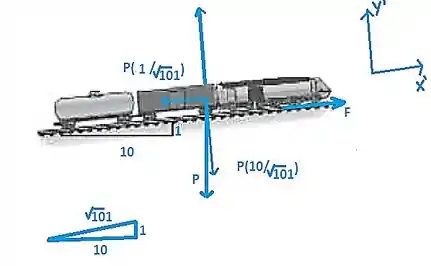
Passo 2
Se o motor exerce uma força de tração que é igual a 1 do peso do trem, podemos chegar ao seguinte valor para a força de tração:
(1kN
Passo 3
O objetivo é encontrarmos a velocidade do trem quando ele tiver avançado uma distância de km aclive acima. Podemos verificar que trem se move a uma aceleração constante, portanto, iremos calcular primeiramente a aceleração do trem e depois encontrar sua velocidade utilizando a equação de torriceli:
Sabendo que o trem parte do repolso ( e que km m, Temos:
Resposta
A velocidade do trem quando ele tiver avançado uma distância de km aclive acima será igual a