Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 12.Problemas - Ex. 213
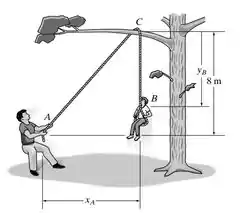
O homem puxa o garoto para cima do galho da árvore C ao caminhar para trás. Se ele parte do repouso quando xA= 0 e se desloca para trás com uma aceleração constante aA= 0,2 m/s2, determine a velocidade escalar do garoto no instante yB= 4 m. Despreze o tamnho do galho. Quando x4=0 , yb=8 m, de maneira que A e B são coincidentes, ou seja, a corda tem 16 m de comprimento.
Passo 1
Primeiramente, deve-se obter uma função que relacione os deslocamentos do homem (representado por xA) e do garoto ( representado por yB). Têm-se que o comprimento total da corda (l) é dado por:
(1)
E que a distância entre os pontos A e C é obtido pela seguinte relação pitagórica:
(2)
Então, a relação entre os deslocamentos é dada ao se substituir (2) em (1), de forma que:
(3)
Passo 2
De posse da função que rege os deslocamentos, sabe-se qua as velocidades instantâneas serão as taxas de deslocamentos nos pontos pelo tempo, de forma que:
Ao realizar a derivada de (3) no tempo, temos que:
(4)
Passo 3
De posse do deslocamento xA e da velocidade vA no instante em que yB= 4 m , podemos obter a velocidade da criança, vB , de acordo com (4).
Resposta
A velocidade será :
