Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 15.Problemas - Ex. 191

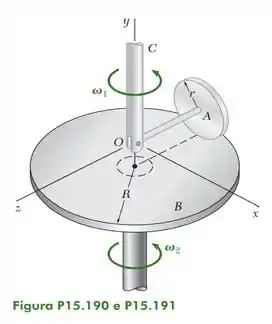
No sistema mostrado na figura, o disco A é livre para girar sobre a barra horizontal AO. Considerando que Considerando que o eixo OC e o disco B giram com velocidades angulares constantes ω 1 e ω 2 respectivamente, ambas no sentido anti-horário, determine (a) a velocidade angular do disco A, (b) a aceleração angular do disco A.

Passo 1

Bora pra questão 191 agora, meus caros (as)!

  1. Do disco A ,temos uma rotação em O:

    2. ω y = ω 1

    ω A = ω x i + ω 1 j + ω 2 k

    Sendo o ponto D o ponto de contato da roda e o disco:

    r D / O = - r j - R k

    V D = ω A × r D / O

    V D = i j k ω x ω 1 ω z 0 - r - R

    V D = - R ω 1 + r ω z i + R ω 1 j - r ω x k

    No disco B

    ω B = ω 2 j

    V D = ω B × r D / O

    V D = ω 2 j × - r j - R k

    V D = - R ω 2 i

    Igualando a velocidade em D:

    - R ω 1 + r ω z i + R ω 1 j - r ω x k = - R ω 2 i

    k = - r ω x = 0 ,     ω x = 0

    i = - R ω 1 + r ω z = - R ω 2 ,       ω z = R r ( ω 1 - ω 2 )

    Portanto a velocidade angular em A é:

    ω A = ω 1 j + R r ( ω 1 - ω 2 ) k

    Passo 2

  2. Aceleração angular é dada pelo disco A em girando em torno do eixo y á taxa ω 1

α A = d ω A d t = ω y × ω A = ω 1 j × ω 1 j + R r ω 1 k

α A = R r ω 1 ( ω 1 - ω 2 ) i

Portanto, a aceleração angular no disco A é

α A = R r ω 1 ( ω 1 - ω 2 ) i

Pronto! Terminamos aqui!

Resposta

  1. ω A = ω 1 j + R r ( ω 1 - ω 2 ) k
  2. R r ω 1 ( ω 1 - ω 2 ) i .
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule a velocidade angular ω da barra esbelta A B como uma função da distância x e da velocidade angular constante ω 0 do tambor.
Um quebra-molas está sendo instalado em uma estrada horizontal para lembrar aos motoristas do limite da velocidade existente. Se o motorista do carro sente em G uma aceleração vertical da mesma ordem
Em um mecanismo projetado para converter movimento linear em movimente angular, o cilindro hidráulico fornece ao pino A uma velocidade constante para baixo v durante um curto intervalo de movimento. D
A rotação da alavanca O A é controlada pelo movimento do disco em contato cujo centro recebe uma velocidade horizontal v . Determine a expressão para a velocidade angular ω da alavanca O A em termos d
O carretel gira sobre seu cubo subindo o cabo interno A enquanto a placa compensadora B puxa os cabos externos para baixo. Os três cabos estão firmemente enrolados em torno de suas respectivas perifer