Enunciado
Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 13.Problemas de Revisão - Ex. 201
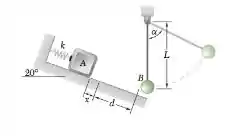
Um bloco A de 2 kg é empurrado contra uma mola comprimindo a na distância x = 0,1 m. O bloco é então liberado do repouso e desliza num declive de 20° até atingir uma esfera B de 1 kg que está suspensa por uma corda inextensível de 1 m. A constante da mola k = 800 N/m, o coeficiente de atrito entre A e o chão é de 0,2, a distância que A desliza após o comprimento indeformado da mola é d = 1,5 m e o coeficiente entre A e B é 0,8. Quando , determine a velocidade de B, e a tração na corda.
Passo 1
Oi oi, meu xuxuzinho!! Tudo bem com você?? Como foi de fim de ano?? Preparado para voltar?? Então vamos lá Vamos analisar o que a nossa questão nos pede e matar essa em 10 minutos?? Bora. Bom, nosso enunciado nos pede para analisarmos a figura e dizermos quais são a velocidade e a tração. Parece muita coisa, mas é tranquilo. Partiu??
Passo 2
Ok, vamos relembrar que a quantidade de movimento linear de uma partícula foi definida como o produto de sua massa m e de sua velocidade v, assim como a aplicação do Coeficiente de Restituição, que relaciona às velocidades relativas de dois corpos antes e depois do impacto, e o Princípio do Impacto Central Oblíquo. Com isso, a partir desse ponto, determinaremos a velocidade de B e a tração da mola.
Aplicaremos, então, o Princípio de Trabalho e Energia:
Eaii?? Chegou bem até aqui?? Então bora substituir os valores e continuar nossa conta.
Aplicando a 2ª Lei de Newton, temos:
Esfera B: sobe o plano inclinado. Usaremos aqui conservação de energia:
Passo 3
Pronto!! Agora é só fazermos umas matemágicas aí pra achar o resultado!!
Vamos determinar a tração: