Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 5.Problemas - Ex. 46
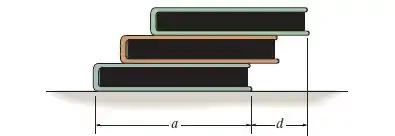
Três livros uniformes, cada um com peso e comprimento , são empilhados como na figura. Determine a distância máxima que o livro do topo pode estender-se em relação ao da base, de modo que a pilha não tombe.
Passo 1
E aí Pessoal, tudo bem? Vamos dar início a mais uma questão juntos!
A ideia nesta questão é determinar qual a máxima distância do terceiro livro para o primeiro para que a pilha permaneça fixa!
Precisamos começar devagar, analisando apenas o caso dos dois livros de cima apenas. Devemos maximizar esta distância primeiro para maximizarmos .
A distância máxima do de cima em relação ao livro abaixo é da metade do seu comprimento, conforme podemos ver na figura abaixo.
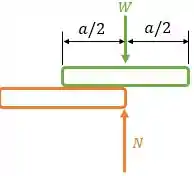
É necessário que isto ocorra para que o centro de gravidade do livro acima (ponto em que atua a força peso), seja colinear com a normal do livro abaixo. Se isto não ocorresse, teríamos um momento de binário!
Em outras palavras, o livro ia rotacionar e iria cair!
Passo 2
Agora vamos analisar o caso para os três livros!
O procedimento é muito semelhante ao caso anterior, só que com um livro a mais. Posicionando a força peso dos dois livros e a normal no livro mais baixo, teremos o seguinte diagrama de equilíbrio:
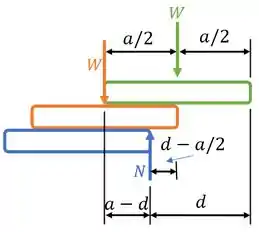
Como os três livros estão em equilíbrio, o somatório de momentos é igual a zero. Realizando esta soma em torno do ponto de aplicação da força normal, temos:
E assim finalizamos a questão!