Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 5.Problemas - Ex. 41
Determine a rigidez de cada mola de modo que a força de 30 N faça com que o elemento sem peso se incline de quando a força é aplicada. Originalmente, o elemento está horizontal e as molas não estão esticadas.
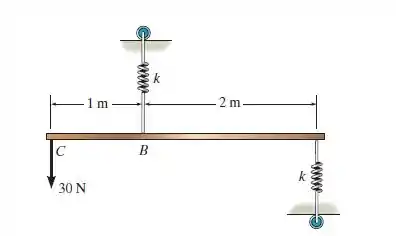
Passo 1
E aí Pessoal, tudo bem? Vamos dar início a mais uma questão juntos!
Esta questão é uma continuidade da questão . Portanto, vamos utilizar todas as relações desenvolvidas lá para resolvermos a nossa questão.
Aqui nós sabemos quem é o ângulo , mas não sabemos quem é a deformação na mola . As forças e continuam as mesmas, já que a geometria da barra e a força não mudou.
Portanto, o que devemos fazer nesta questão é quase que o inverso da questão anterior.
Se a gente já sabe quem é , vamos determinar a distância ! Com este valor, podemos determinar as deformações e . E por fim, chegamos à rigidez .
Então, vamos as contas!
Passo 2
Vamos começar utilizando a relação entre o ângulo e a distância ! Relembrando,
Só que nós sabemos que e ! Substituindo estas duas relações, temos:
E portanto, a deformação (ou ) será:
E a rigidez será:
E assim finalizamos a questão!