Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 1.Problemas - Ex. 39
Um tubo de aço de 300mm de diâmetro externo é fabricado com chapa de 6,35mm de espessura, por meio de um cordão de solda ao longo de uma hélice que forma um ângulo de com um plano perpendicular ao eixo do tubo. Sabendo-se que uma força axial P de 270KN é aplicada ao tubo, determine as tensões, normal e de cisalhamento, que atuam respectivamente nas direções normal e tangencial, ao cordão de solda.
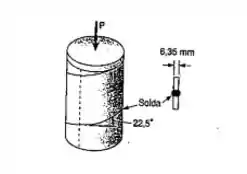
Passo 1
Vamos fazer um desenho e dar uma olhada em como se distribuem as forças no plano que nos interessa.
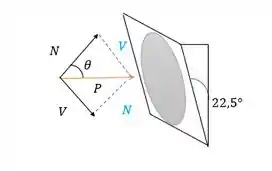
Onde , e pela geometria do problema a gente consegue observar que ele esta entre P e N.
Quando temos o ângulo dessa forma, a decomposição das forças se dá:
Passo 2
A área sofrera distorção, e é parecido com o que acontece com uma seção retangular. Somente a vertical distorce, assim:
Onde é o diâmetro distorcido e é o diâmetro inicial.
O plano oblíquo será então uma elipse, pois na horizontal o diâmetro não se distorce.
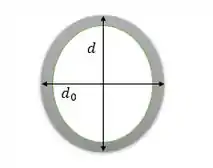
Precisaremos das medidas internas por se tratar de um tubo:
Enfim as áreas:
E a área final será:
Outro jeito seria ter feito a área da coroa circular e dividi-la pelo cosseno do ângulo.
Passo 3
Agora que temos a área que nos interessa vamos encontrar as tensões:
E para a tensão cisalhante: