Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 1.Problemas - Ex. 29

Para a montagem e carregamento do problema 1.13, determine (a) a tensão de cisalhamento média no pino B; (b) a tensão de esmagamento em B, na barra de ligação BE; (c) A tensão de esmagamento em B, na barra ABCD, sendo que esta barra tem seção transversal retangular de 15x50mm.

Dados: diâmetro do pino B = 14mm, Barra BE: 10x40mm.

Passo 1

O item (a) pede a tensão cisalhante no pino B. Primeiro precisamos calcular os esforços na seção do pino. Para isso vamos fazer um diagrama de corpo livre da barra EFG, arbitrando as forças que não conhecemos.

Vamos usar as equações de equilíbrio, nesse caso é importante que nós encontremos a força F E B . Usando a equação do equilíbrio dos momentos no ponto F e considerando o sentido horário positivo teremos:

∑ M = 400 F E B + 250 P = 0

F E B = - 250 P 400

O sinal negativo significa que a força tem sinal oposto ao que foi arbitrado, podemos corrigir invertendo no desenho ou sinalizando com uma seta. Com P= 24 temos:

F E B = 15 K N ( ↓ )

Passo 2

Vamos transferir a força para a barra vertical EG, que nos interessa. Se liga aqui, para transferir o esforço a gente inverte o sentido.

Descobrimos que a força é para baixo e transferimos ela para cima, agora vamos ao cálculo da tensão no pino B.

τ = F A

Usaremos a área da face do pino pois é paralela ao esforço.

A = π d 2 4 = 153,94 m m ²

Como o pino tem duas faces, temos duas áreas.

2 A = 307,88 m m ²

Convertendo a força de KN para N, teremos nosso resultado em MPa e isso nos interessa.

15 K N = 15 × 10 ³ N

τ = 15 × 10 3 307,88 = 48,72 M P a

Passo 3

Para o item b, é solicitada a tensão na barra BE, no ponto B. Aqui devemos prestar bastante atenção, vamos desenhar a área da seção transversal do ponto B e dar uma boa olhada.

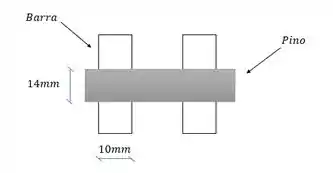
As áreas que sofrem esmagamento na barra são parte do pino, que faz uma abertura de 14mm ao longo dos 10mm de barra. Como são duas barras a área é:

A = 2 × 10 × 14 = 280 m m ²

E enfim a tensão de esmagamento nesse ponto da barra é:

τ = F A = 15 × 10 3 280 = 53,6 M P a

Passo 4

Finalmente para o item c, faremos bem parecido com o item b. O ponto B na barra ABCD é em cima do pino. Se a gente fizer um desenho da seção transversal vai ficar dessa forma:

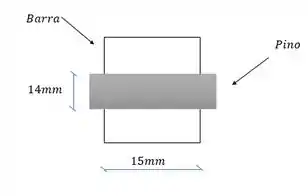
A área que sofre esmagamento é o retângulo com a espessura da barra e altura do diâmetro do pino, assim:

A = 210 m m ²

E enfim:

τ = F A = 15 × 10 3 210 = 71,43 M P a

Resposta

τ = 48,72 M P a

τ = 53,6 M p a

τ = 71,43 M p a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Resolva o Problema 2.109 supondo que os cabos foram substituídos por barras com a mesma área de seção transversal e o mesmo material. Supondo ainda que as barras foram fixadas de modo que possam supor
Resolva o Problema 2.113 supondo que a intensidade da força Q aplicada em B seja aumentada gradualmente de zero até 260k N e depois diminuída de volta para zero. Sabendo que a = 0,640m , determine (a)
Para a barra composta do Problema 2.111, se P é gradualmente aumentada desde zero até 436k N e depois diminuída até zero, determine (a) a deformação máxima da barra, (b) a tensão máxima nas barras de
Para a barra composta do Problema 2.107, se P é aumentada gradualmente desde zero até que o deslocamento do ponto C atinja um valor máximo de δ m = 0,3m m e depois diminuída novamente até zero, determ
Duas barras de aço temperado, cada uma com espessura de 5 mm, são coladas a uma barra de aço doce de 12 mm. Essa barra composta é submetida a uma força axial centrada de intensidade P, conforme mostra